Tabla de Contenidos
Examen (Parcial) - 61.10. Analisis Matemático III A
Cátedra: Isaacson
Fecha: 22/06/06 3° Fecha - (1° Cuatrimestre 2006
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- Sea
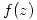 analítica en
analítica en 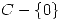 tal que
tal que 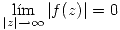 . Mostrar que la serie de Laurent de
. Mostrar que la serie de Laurent de  alrededor de
alrededor de  solo tienen términos con potencias de
solo tienen términos con potencias de 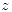 negativas.
negativas. - Si
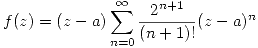 y
y 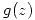 es analítica salvo en
es analítica salvo en  donde tienen un polo simple con residuo
donde tienen un polo simple con residuo 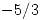 , analizar qué tipo de singularidad es
, analizar qué tipo de singularidad es 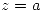 para
para 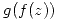 y hallar
y hallar ![<tex>\mbox{Res}[g(f(z)),z=a]</tex> <tex>\mbox{Res}[g(f(z)),z=a]</tex>](lib/plugins/latex/images/ef2a03f0a87c3cdc9c8d426433d0387b30e9eb2c_0.png)
- Transformar la región
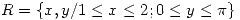 a tra vez de la función
a tra vez de la función 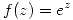
- Sea la función
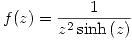 .
.- Clasificar la singularidad en el origen.
- Calcular la integral
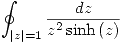
Resolución
Punto I
Si f(z) es analitica para |z|>0 entonces en el entorno de z=0 f(z) se puede escribir como:
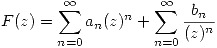 Si tomo el módulo a cada lado de la igualdad:
Si tomo el módulo a cada lado de la igualdad:
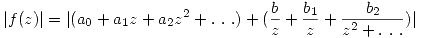 Por la desigualdad de :
Por la desigualdad de :
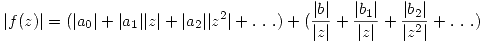
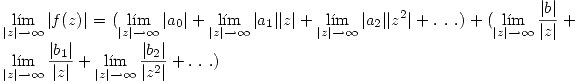
Todos los terminos de potencias negativas tienden a cero cuando z se acerca al infinito.
Para que la condicion inicial de 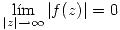 se cumpla entonces se debe cumplir que los
se cumpla entonces se debe cumplir que los 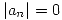 .
.
La ecuación inicial se puede escribir:
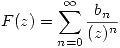
Punto II
Escribo a 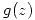 como
como 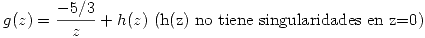 .
.

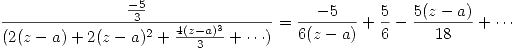
entonces:
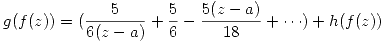
Como lo definí al comienzo, 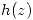 no tiene singularidades en
no tiene singularidades en 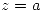 , a lo sumo tendrá ceros.
Puedo decir entonces que
, a lo sumo tendrá ceros.
Puedo decir entonces que 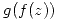 tiene un polo simple en
tiene un polo simple en 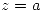 y el
y el ![<tex>\mbox{Res}[g(f(z)),z=a]=\frac{-5}{6}</tex> <tex>\mbox{Res}[g(f(z)),z=a]=\frac{-5}{6}</tex>](lib/plugins/latex/images/cb1e0def4a695e2a489bc6dc0ed270f81f097265_0.png)
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
