Tabla de Contenidos
Primer Parcial 05/07/2005 - Cátedra Isaacson
Enunciado
- Calcular la integral
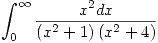 . Justificar.
. Justificar. - Hallar los tres primeros términos del desarrollo en serie de la función
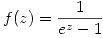 alrededor de
alrededor de  y determinar la región de convergencia.
y determinar la región de convergencia. - Calcular
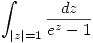 .
.
- Transformar la región
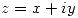 , con
, con 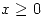 e
e 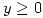 , a través de la función
, a través de la función 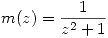 .
. - Sea
 entera,
entera, 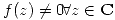 y
y 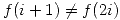 , ¿Qué puede decir sobre su desarrollo en serie? ¿Qué tipo de singularidad tiene en
, ¿Qué puede decir sobre su desarrollo en serie? ¿Qué tipo de singularidad tiene en 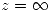 ?
? - Si
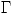 es la curva que limita una región
es la curva que limita una región  , hallar la relación entre
, hallar la relación entre 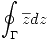 y el área de
y el área de  .
.
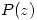 es un polinomio de grado
es un polinomio de grado  que no tiene ceros en
que no tiene ceros en  ,
, 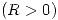 . Si
. Si 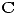 es la circunferencia
es la circunferencia 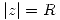 , calcule
, calcule 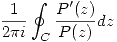 .
.
Resolución
Punto I
Sabiendo que 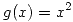 ,
, 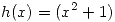 y
y 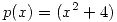 son funciones pares se puede afirmar que:
son funciones pares se puede afirmar que:
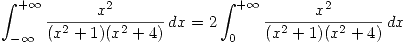
Por lo tanto resulta conveniente calcular:
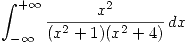
Para ello se pasa a la variable compleja de la siguiente manera:
![<tex>\oint_{\gamma_r} f(z)\, dz = \oint_{\gamma_r} \frac{z^2}{(z^2 + 1)(z^2 + 4)}\, dz = 2\pi i \sum_{n = 1}^k \mathnormal{Res} [f(z),z_n]</tex> <tex>\oint_{\gamma_r} f(z)\, dz = \oint_{\gamma_r} \frac{z^2}{(z^2 + 1)(z^2 + 4)}\, dz = 2\pi i \sum_{n = 1}^k \mathnormal{Res} [f(z),z_n]</tex>](lib/plugins/latex/images/c1bb06c8a04ce43f61a5469c9bc4e6a1642b5bc1_0.png)
Conociendo las singularidades 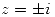 Y
Y  .Se calculan los residuos según el gráfico en
.Se calculan los residuos según el gráfico en  y
y 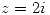 :
:
Para 
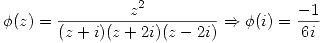
Para 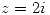
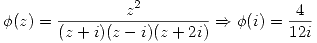
![<tex>\Rightarrow 2\pi i \sum_{n = 1}^k \mathnormal{Res} [f(z),z_n] = 2\pi i(\frac{-1}{6i}+\frac{4}{12i}) = \frac{\pi}{3}</tex> <tex>\Rightarrow 2\pi i \sum_{n = 1}^k \mathnormal{Res} [f(z),z_n] = 2\pi i(\frac{-1}{6i}+\frac{4}{12i}) = \frac{\pi}{3}</tex>](lib/plugins/latex/images/c41d2d062ccbc442e0bdb27850fd6c32abacb0bc_0.png)
Sabiendo que:
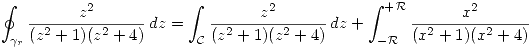
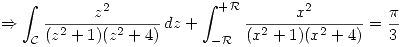
Si hacemos el cambio de variable 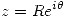 obtenemos:
obtenemos:
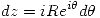
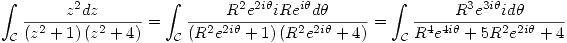
Y si tomamos el límite para cuando 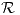 tiende a infinito:
tiende a infinito:
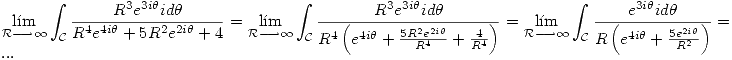
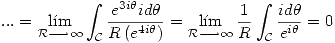
Entonces, cuando  tiende a infinito,
tiende a infinito, 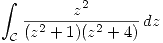 tiende a cero.
tiende a cero.
Por lo tanto queda:
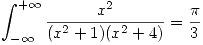
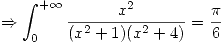
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

