Tabla de Contenidos
Examen (Parcial) - 61.10. Análisis Matemático III
Cátedra: Murmis
Fecha: 1er Oportunidad - (2do Cuatrimestre) 2008
Día: 29/10/2008
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- P1) Uniformizar

- P2) Resolver:
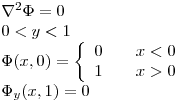
- P3) Analizar convergencia y calcular
![<tex>\int_{0}^{+\infty}\frac{\sqrt[3]{x}}{{(x+1)}^2(x+3)} \, dx</tex> <tex>\int_{0}^{+\infty}\frac{\sqrt[3]{x}}{{(x+1)}^2(x+3)} \, dx</tex>](lib/plugins/latex/images/6e8f4c543d9dc586bd13bb2f2b74d3146212812a_0.png)
- T1) Demostrar el teorema de unicidad de la Serie de Laurent.
- T2) Demostrar si es verdadero o falso
![<tex>f(z) \in H/z_{\infty} \Rightarrow R \left[f(z);z_\infty \right] = 0</tex> <tex>f(z) \in H/z_{\infty} \Rightarrow R \left[f(z);z_\infty \right] = 0</tex>](lib/plugins/latex/images/93b617d48803a720cfd8c910ab6a14c4df23e769_0.png)
- T3) Dado
![<tex> \left. \begin{array}{ll} z_0 \mbox { es polo de segundo orden de } f(z) \\ \gamma_z : z = z_0 + re^{it} \qquad t \in [0,2\pi] \\\end{array} \right\} </tex> <tex> \left. \begin{array}{ll} z_0 \mbox { es polo de segundo orden de } f(z) \\ \gamma_z : z = z_0 + re^{it} \qquad t \in [0,2\pi] \\\end{array} \right\} </tex>](lib/plugins/latex/images/098fd3076fbd2af19933c71cbf7c6dbafc4f7f15_0.png) , decir cuánto vale
, decir cuánto vale 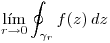
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá o envíame un PM.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
