Análisis Matemático III - Curso Ing. Murmis
2007 - 1er cuatrimestre - 1er Parcial - 2da oportunidad - 30/05/07
- P1) Si
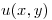 es armónica, hallar su conjugada
es armónica, hallar su conjugada
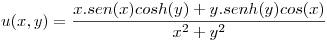
- P2) Dada
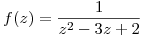 hallar un desarrollo en Serie de Laurent válido en
hallar un desarrollo en Serie de Laurent válido en 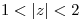 .
. - P3) Analizar la convergencia y calcular el VP
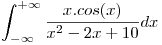
- T1) Demostrar si es verdadero o falso:
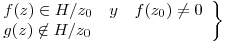 ⇒
⇒ 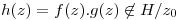
- T2) Demostrar si es verdadero o falso
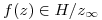 ⇒
⇒ ![<tex>R[f(z);z_{\infty}] = 0</tex> <tex>R[f(z);z_{\infty}] = 0</tex>](lib/plugins/latex/images/9b6aeb01d0e14baaa6e2798bfcbc5a2b555e92d0_0.png)
- T3) Analizar cuantos resultados distintos tiene la integral
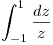 y calcularlos.
y calcularlos.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
