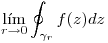Análisis Matemático III - Curso Ing. Murmis
2007 - 1er cuatrimestre - 1er Parcial - 1ra oportunidad - 16/05/07
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

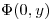 sobre la cara aislada.
sobre la cara aislada. 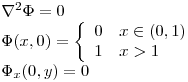

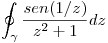

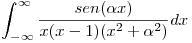
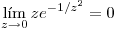
 . ¿Es conforme?.
. ¿Es conforme?.![<tex> \left. \begin{array}{ll} z_0 \mbox { es polo de segundo orden de } f(z) \\ \gamma_z : z = z_0 + re^{it} \mbox{ } t \in [0,2\pi] \\\end{array} \right\} </tex> <tex> \left. \begin{array}{ll} z_0 \mbox { es polo de segundo orden de } f(z) \\ \gamma_z : z = z_0 + re^{it} \mbox{ } t \in [0,2\pi] \\\end{array} \right\} </tex>](lib/plugins/latex/images/050c3be89d1c6e83cd3a2bf2740db704c40050f9_0.png) , decir cuánto vale
, decir cuánto vale