Análisis Matemático III - Curso Ing. Murmis [Foros-FIUBA::Wiki]

Traza: • Análisis Matemático III - Curso Ing. Murmis • Análisis Matemático III - Curso Ing. Murmis

Estás aquí: Wiki » Materias » Departamento de Matemática » 61.10. Análisis Matemático III A » Análisis Matemático III - Curso Ing. Murmis

Análisis Matemático III - Curso Ing. Murmis

2001 - 1er cuatrimestre - 1er Parcial - 1ra oportunidad - Tema 2 - 10/05/2000

P1) Si 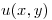$<tex>u(x,y)</tex>$ es armónica, hallar su conjugada

$<tex>u(x,y)=\frac{x.sen(x)e^x+2y.senh(y)cos(x)+x.sen(x)e^{-x}+2x^3y+2xy^3}{x^2+y^2}</tex>$

P2) Calcular $<tex>\oint_{|z|=2} \frac{1-e^z+z}{z^3(z-1)^2}dz</tex>$
P3) Analizar la convergencia y calcular $<tex>I(a,b)= \int_{0}^{+\infty}\frac{x^a}{b^2+x^2}dx</tex>$
T1) Demostrar si es verdadero o falso: $<tex>\lim_{z \to 0}z.e^{-1/z^2}=0</tex>$
T2) Demostrar que la ecuación de Laplace se conserva por una transformación conforme.
T3) Determinar para qué valores de z es cierta la siguiente expresión:

$<tex>\frac{1}{(z-2)^2}=\sum_{n=0}^{+\infty}(-1)^n(n+1)\frac{(i-2)^n}{(z-i)^{n+2}}</tex>$

materias/61/10/parcial_3_20000510_2.txt · Última modificación: 2007/08/11 10:16 por gsoriano

Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported