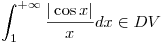Análisis Matemático III - Curso Ing. Murmis
1999 - 2do cuatrimestre - 1er Parcial - 3ra oportunidad - 20/12/1999
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

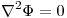 en D y encontrar
en D y encontrar 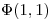

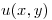 es armónica, hallar su conjugada:
es armónica, hallar su conjugada: 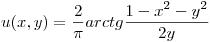
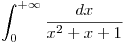
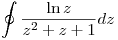
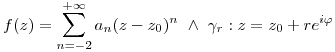 ⇒
⇒ 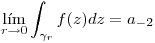
![<tex>\varphi \in [0,\alpha] ; \alpha , 2\pi</tex> <tex>\varphi \in [0,\alpha] ; \alpha , 2\pi</tex>](lib/plugins/latex/images/13af504c19aeecb3c6de485dcfa0d0eebc8ed2b6_0.png)
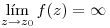 ⇒
⇒ 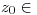 polo de
polo de