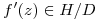Análisis Matemático III - Curso Ing. Murmis
1999 - 1er cuatrimestre - 1er Parcial - 2da oportunidad - 19/05/99
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

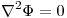 en D y encontrar
en D y encontrar 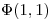

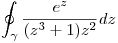

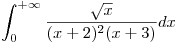
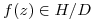 ⇒
⇒