Tabla de Contenidos
Parcial 9/05/2006 - Cátedra Anaya
Enunciado
- Dadas las regiones
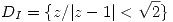 ,
, 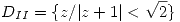 ,
, 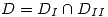 Encontrar una función armónica en
Encontrar una función armónica en  cuyo valor en la parte de la frontera correspondiente a
cuyo valor en la parte de la frontera correspondiente a 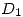 sea constante igual a 1 y en la correspondiente a
sea constante igual a 1 y en la correspondiente a 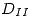 sea 2. Indicar si la función hallada es única. Justificar.
sea 2. Indicar si la función hallada es única. Justificar. - Encontrar el desarrollo de Laurent en potencias de
 de
de 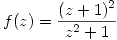 convergente en
convergente en 
- Caracterizar la Serie de Laurent en torno a
 de las funciónes holomorfas para
de las funciónes holomorfas para 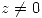 con
con 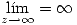 y
y 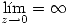
- Clasificar las singularidades de
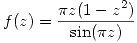 en
en 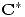 y informar acerca del
y informar acerca del 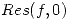 ,
, 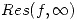
- Calcular
![<tex>\oint_\gamma \sqrt[3]{z-1} \frac{f(z)}{z} </tex> <tex>\oint_\gamma \sqrt[3]{z-1} \frac{f(z)}{z} </tex>](lib/plugins/latex/images/32566d8d5e08842528adc27ecdec3c8d312ef0ac_0.png) siendo
siendo 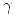 la circunferencia
la circunferencia 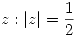 orientada en sentido antihorario, y si se considera la determinación de
orientada en sentido antihorario, y si se considera la determinación de ![<tex>\sqrt[3]{z}</tex> <tex>\sqrt[3]{z}</tex>](lib/plugins/latex/images/7ece6e7853e7985ff349be53daf9720761acb340_0.png) holomorfa en
holomorfa en 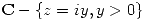 cuyo valor en 8 es 2.
cuyo valor en 8 es 2.
- Estudiar la convergencia de la integral
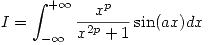
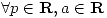
- Calcular la integral para
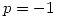
- Sea
 una sucesión en
una sucesión en 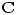 tal que existe
tal que existe 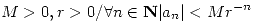
Encontrar un entorno de en el que
en el que 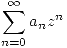 defina una función holomorfa. Justificar.
defina una función holomorfa. Justificar.
Resolución
Resolución Ejercicio 2
a)
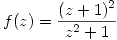
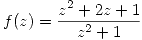
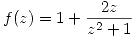
Voy a llamar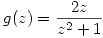
Por lo tanto sacando como factor comun en el denominador a 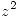 queda:
queda: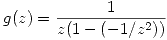
Esta funcion la puedo expresar como serie geométrica siempre y cuando 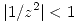
Por lo tanto  que es la región que me estaban pidiendo
que es la región que me estaban pidiendo
Entonces 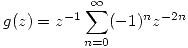
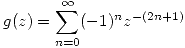
Nosotros teniamos que 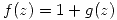
Por lo tanto:
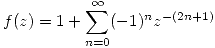
b)
Que la función holomorfa tenga límite infinito en el origen y en el punto infinito, significa que en esos puntos estan los polos de la función.
Suponiendo que 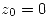 es un polo de orden k y el
es un polo de orden k y el 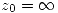 es un polo de orden j. Por la definición de polo podemos representar a una serie de este estilo como:
es un polo de orden j. Por la definición de polo podemos representar a una serie de este estilo como:
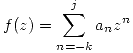
Queda pendiente la resolución para la próxima entrega, y gracias al que cambió el estilo del enunciado.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
