Examen Parcial - 61.10. Análisis Matemático III - 28/11/2007
- Enunciado
  - Punto I
  - Punto II
  - Punto III
  - Punto IV

2007

Cátedra: Sacerdoti Fecha: 3ra Oportunidad - 2do Cuatrimestre 2007 Día: 28/11/2007

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Punto I

Dada la I.I.

$<tex>\int_0^\infty \frac{ x^a} { (1 + x^2)^2} \, dx</tex>$

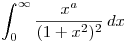
a) Hallar todos los valores de a para los cuales la integral es convergente

b) Calcularla en el campo complejo

c) Calcularla mediante Eulerianas

Punto II

Dada la función 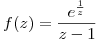$<tex>f(z) = \frac {e^\frac{1}{z} }{z - 1}</tex>$ ; calcular 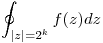$<tex>\oint_{|z|=2^k} f(z) dz</tex>$ , para k = -1,0,1

Punto III

Hallar la distribución de potencial P en la región exterior a ambos círculos. Hallar su expresión y graficar las líneas equipotenciales y de campo.

Punto IV

Determinar si son verdaderas las siguientes afirmaciones. Justificar.

a) Sea 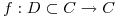$<tex> f: D \subset C \rightarrow C</tex>$ , tal que 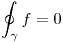$<tex>\oint_{\gamma} f = 0</tex>$ para todo lazo 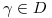$<tex>\gamma \in D </tex>$ , entonces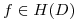 $<tex>f \in H(D)</tex>$

b) 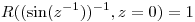$<tex> R( ({\sin (z^{-1}}))^ {-1} , z = 0 ) = 1</tex>$

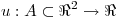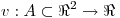c) Sean $<tex>u : A \subset {\Re}^2 \rightarrow \Re</tex>$ y $<tex>v : A \subset {\Re}^2 \rightarrow \Re</tex>$ , funciones derivables. Si ellas cumplen las condiciones de Cauchy-Riemman en un punto 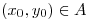$<tex>(x_0, y_0) \in A</tex>$ , entonces se puede afirmar que la funcion 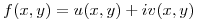$<tex>f(x,y) = u(x,y) + i v(x,y)</tex>$ es diferenciable en $<tex>x_0 + i y_0 </tex>$