Examen Final - 61.10. Analisis Matemático IIIA
Cátedra: Isaacson
Día: 03/03/2009
Enunciado
Punto I
Hallar, si es posible y justificando claramente la respuesta, una función analítica en el semiplano 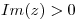 cuya parte real sea solución del siguiente problema:
cuya parte real sea solución del siguiente problema:
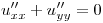 ,
, 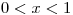 ,
, 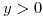
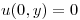 ,
, 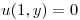
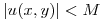 ,
, 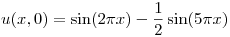
Punto II
a) Sea 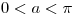 ,
, 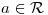 . Hallar la serie de Fourier asociada a
. Hallar la serie de Fourier asociada a 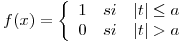
Graficar la extensión periódica de  y analizar convergencia.
y analizar convergencia.
b) Hallar 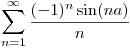
c) Hallar 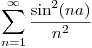
Punto III
Si  y
y 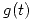 son de cuadrado integrable:
son de cuadrado integrable: 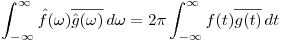 .
.
a) Hallar la transformada de Fourier de 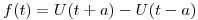
b) Usar lo anterior para calcular 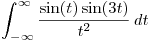
Punto IV
a) Mostrar, estableciendo las hipotesis necesarias, que si ![<tex>\hat f (\omega) = \mathcal{F}[f(t)]</tex> <tex>\hat f (\omega) = \mathcal{F}[f(t)]</tex>](lib/plugins/latex/images/e6c4178238cc75c41a63e48ae08a48aee85ef50c_0.png) , entonces:
, entonces:
b) Sabiendo que  = \frac{2}{1+\omega^{2}}</tex> <tex>\mathcal{F}[e^{-|t|}](\omega) = \frac{2}{1+\omega^{2}}</tex>](lib/plugins/latex/images/cb56d6f4ecb8e33bf200129df20a795bffeb3388_0.png) , usar la parte a) para calcular
, usar la parte a) para calcular ![<tex>\mathcal{F}[\frac{1}{1+t^{2}}]</tex> <tex>\mathcal{F}[\frac{1}{1+t^{2}}]</tex>](lib/plugins/latex/images/57412fe0ca245b2eb3618b19b8b1471cf0d90938_0.png) y
y ![<tex>\mathcal{F}[\frac{t}{(1+t^{2})^{2}}]</tex> <tex>\mathcal{F}[\frac{t}{(1+t^{2})^{2}}]</tex>](lib/plugins/latex/images/23976269e6f65a6f21a818870166a15396d0b164_0.png) .
.
Punto V
a) Hallar la ecuación diferencial y las condiciones iniciales del problema cuya solución es:
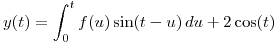
b) Sea 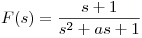 ,
, 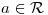 .
.
- Demostrar que si
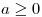
 está acotada y que si
está acotada y que si 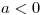 ,
,  no está acotada.
no está acotada. - Comprobar que si
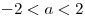 ,
,  es una función oscilante de
es una función oscilante de  . ¿Para que valores de
. ¿Para que valores de  las oscilaciones aumentan con
las oscilaciones aumentan con  y para que valores disminuyen?
y para que valores disminuyen?
c)
Si  y
y 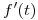 son regulares a trozos y de orden exponencial, la abscisa de convergencia de
son regulares a trozos y de orden exponencial, la abscisa de convergencia de 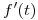 es negativa y si
es negativa y si ![<tex>F(s) = \mathcal{L}[f(t)]</tex> <tex>F(s) = \mathcal{L}[f(t)]</tex>](lib/plugins/latex/images/ffff968ca56f4f60e957117c501d85520134ac9c_0.png) , entonces:
, entonces:
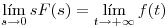
si dichos límites existen.
Analizar si puede aplicarse el resultado anterior a 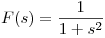 . ¿Por qué?
. ¿Por qué?
Resolución
Punto I
Se resuelve por separación de variables, llamando  o
o 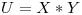 para simplificar.
para simplificar.
”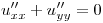 ”, entonces:
”, entonces:
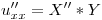 y
y 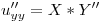
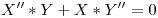 , dividiendo todo por
, dividiendo todo por  (
( ) queda:
) queda:
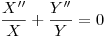 ⇒
⇒ 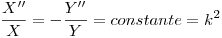 (porque dependen de variables distintas, entonces la división no puede dar otra cosa que una constante).
(porque dependen de variables distintas, entonces la división no puede dar otra cosa que una constante).
Primero resuelvo para 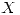 :
:
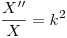 …
… 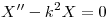 ⇒
⇒ 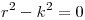 y
y 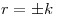
⇒ 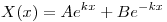
Por las condiciones de contorno:
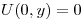 ⇔
⇔ 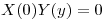 ⇔
⇔ 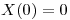 porque si
porque si 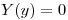 se tendría
se tendría 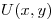 idénticamente nula.
idénticamente nula.
entonces: 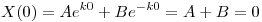 ⇒
⇒  y ahora
y ahora 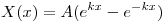
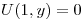 ⇔
⇔ 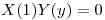 ⇔
⇔ 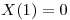 porque si
porque si 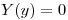 se tendría
se tendría 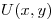 idénticamente nula.
idénticamente nula.
entonces: 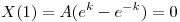 ⇒
⇒ 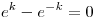 porque si
porque si  se tendría
se tendría 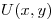 idénticamente nula.
idénticamente nula.
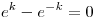 ⇔
⇔  ⇔
⇔ 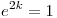 ⇔
⇔ 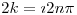 ⇒
⇒ 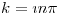 y ahora
y ahora 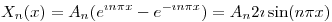
donde 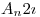 es una constante que depende de
es una constante que depende de 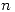 y puedo hacer
y puedo hacer 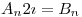 y
y 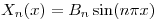
Ahora resuelvo para  :
:
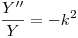 …
… 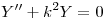 ⇒
⇒ 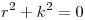 y
y 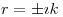
⇒ 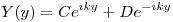 y
y 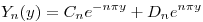
Uso otra de las condición para obtener que:
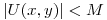 ⇔
⇔ 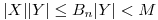 , porque
, porque 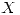 es un seno y está acotada. Entonces la condición de
es un seno y está acotada. Entonces la condición de 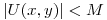 implica que
implica que 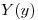 esté acotada.
Como
esté acotada.
Como 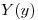 es una combinación lineal de
es una combinación lineal de 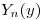 , los términos que aparecen son funciones exponenciales reales, y como la función está definida para
, los términos que aparecen son funciones exponenciales reales, y como la función está definida para 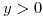 los términos con
los términos con 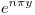 tienen que ser nulos para todo
tienen que ser nulos para todo 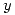 lo que implica
lo que implica 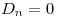 .
.
y ahora 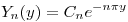 .
.
Con 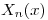 y
y 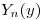 calculadas, reescribo
calculadas, reescribo 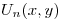 como:
como:
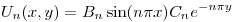 y como
y como 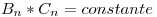 puedo hacer
puedo hacer 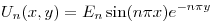
y ahora 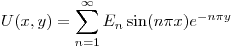
Usando la última condición:
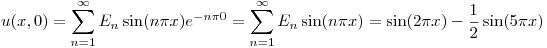 y los coeficientes
y los coeficientes 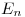 tienen que ser los coeficientes de Fourier del desarrollo en serie de senos de la función
tienen que ser los coeficientes de Fourier del desarrollo en serie de senos de la función 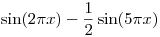 . Pero la función ya es una serie sumatoria de senos, por lo que
. Pero la función ya es una serie sumatoria de senos, por lo que 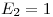 ,
, 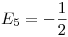 y el resto de los
y el resto de los  es igual a 0.
es igual a 0.
Entonces, la función  queda:
queda:
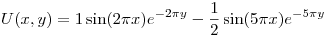
Punto II
a) Gráfico de la función y extensión periódica:
Como se ve en el gráfico se trata de una función par, entonces los coeficientes de Fourier 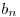 son nulos y los
son nulos y los 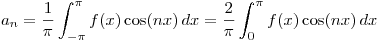 .
.
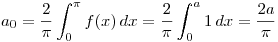
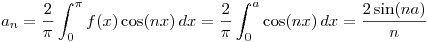
Entonces:
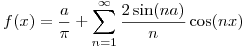
b)
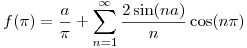 pero
pero 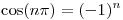 y
y 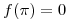 por la definición.
por la definición.
Reemplazando y despejando:
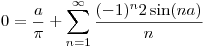 ⇒
⇒ 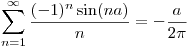
c)
Parseval: 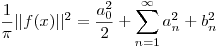
Por un lado: 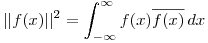 que en este caso es
que en este caso es 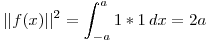
Por otro lado: 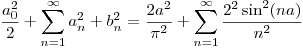
Igualando y despejando:
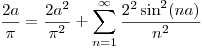
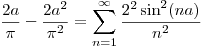
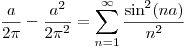
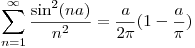
Como  ,
, 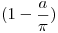 es positivo, que se tiene que cumplir porque se está haciendo una suma de infinitos terminos positivos (
es positivo, que se tiene que cumplir porque se está haciendo una suma de infinitos terminos positivos (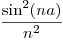 ).
).
Punto III
a)
Primero, el gráfico de  para saber como es la función:
para saber como es la función:
Entonces 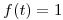 para
para  y
y  para otros valores.
para otros valores.
![<tex>\mathcal{F}[f(t)] = \int_{-\infty}^{\infty} f(t)e^{- \imath \omega t} \,dt = \int_{- a}^{ a} e^{- \imath \omega t} \,dt</tex> <tex>\mathcal{F}[f(t)] = \int_{-\infty}^{\infty} f(t)e^{- \imath \omega t} \,dt = \int_{- a}^{ a} e^{- \imath \omega t} \,dt</tex>](lib/plugins/latex/images/93002f06286467e2a2364653c54fd400e84025c2_0.png)
![<tex>\mathcal{F}[f(t)] = \frac{2sin(\omega a)}{\omega}</tex> <tex>\mathcal{F}[f(t)] = \frac{2sin(\omega a)}{\omega}</tex>](lib/plugins/latex/images/663e8156f6871aa46e7b791454d8a40b6d141c6b_0.png)
b) Puedo reescribir el integrando como:
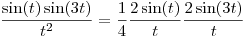 .
.
De esta forma puedo pensar a las fracciones como las transformadas de dos funciones 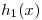 y
y 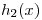 tales que:
tales que:
 y
y ![<tex>\mathcal{F}[h_{1}(x)] = \frac{2 \sin(t)}{t}</tex> <tex>\mathcal{F}[h_{1}(x)] = \frac{2 \sin(t)}{t}</tex>](lib/plugins/latex/images/64ed51bcf06e147f935ba994fae05b7866bb6a08_0.png)
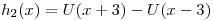 y
y ![<tex>\mathcal{F}[h_{2}(x)] = \frac{2 \sin(3t)}{t}</tex> <tex>\mathcal{F}[h_{2}(x)] = \frac{2 \sin(3t)}{t}</tex>](lib/plugins/latex/images/a2bdcf6a6f045c2eb102cacd3c24eae787048d17_0.png)
Usando el teorema de la definición y lo anterior:
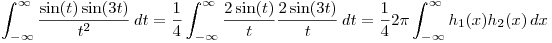 .
.
El producto de 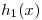 con
con 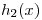 se puede ver en el gráfico que sigue:
se puede ver en el gráfico que sigue:
Además, las funciones 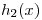 y
y 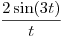 son reales, por lo que conjugarlas da las mismas funciones.
son reales, por lo que conjugarlas da las mismas funciones.
Para terminar:
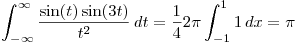 .
.
Punto IV
a) Son demostraciones, en la teórica deberían haberlas dado o deberían estar en algun libro, pero resuelvo la primera porque no me acuerdo que se haya dado en clase.
Como ![<tex>\hat f (\omega) = \mathcal{F}[f(t)]</tex> <tex>\hat f (\omega) = \mathcal{F}[f(t)]</tex>](lib/plugins/latex/images/e6c4178238cc75c41a63e48ae08a48aee85ef50c_0.png) ,
, 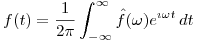 ⇒
⇒ 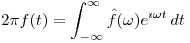
⇒ 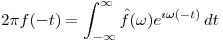
Por otro lado:
![<tex>\mathcal{F}[\hat f (\omega)] = \int_{-\infty}^{\infty} \hat f (\omega) e^{- \imath x \omega} \,d\omega</tex> <tex>\mathcal{F}[\hat f (\omega)] = \int_{-\infty}^{\infty} \hat f (\omega) e^{- \imath x \omega} \,d\omega</tex>](lib/plugins/latex/images/8c765cb02427d9d363bed41d4a185bf8c763216a_0.png) y como
y como 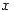 y
y  toman todos los valores reales, puedo reemplazar
toman todos los valores reales, puedo reemplazar 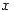 por
por  :
:
![<tex>\mathcal{F}[\hat f (\omega)] = \int_{-\infty}^{\infty} \hat f (\omega) e^{- \imath t \omega} \,d\omega</tex> <tex>\mathcal{F}[\hat f (\omega)] = \int_{-\infty}^{\infty} \hat f (\omega) e^{- \imath t \omega} \,d\omega</tex>](lib/plugins/latex/images/af15dc08c87c8f5fc41b3aa8c4ff9b314cc6a897_0.png)
Comparando los resultados se ve que coinciden y queda demostrado.
b)
![<tex>\mathcal{F}[\frac{1}{1+t^{2}}]</tex> <tex>\mathcal{F}[\frac{1}{1+t^{2}}]</tex>](lib/plugins/latex/images/57412fe0ca245b2eb3618b19b8b1471cf0d90938_0.png) :
:
Puedo pensar que 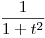 es la transformada de Fourier de una función
es la transformada de Fourier de una función 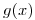 , entonces
, entonces 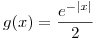
Usando la primer propiedad del ejercicio anterior:
![<tex>\mathcal{F}[\frac{1}{1+t^{2}}] = 2 \pi \frac{e^{-|-x|}}{2} = \pi e^{-|x|}</tex> <tex>\mathcal{F}[\frac{1}{1+t^{2}}] = 2 \pi \frac{e^{-|-x|}}{2} = \pi e^{-|x|}</tex>](lib/plugins/latex/images/d47815d80eda045a0245563feb3f81fa1effdb95_0.png) .
.
![<tex>\mathcal{F}[\frac{t}{(1+t^{2})^{2}}]</tex> <tex>\mathcal{F}[\frac{t}{(1+t^{2})^{2}}]</tex>](lib/plugins/latex/images/23976269e6f65a6f21a818870166a15396d0b164_0.png) :
:
Primero hay que darse cuenta que: 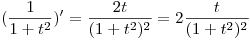
Usando la 2da propiedad:
![<tex>\mathcal{F}[\frac{2t}{(1+t^{2})^{2}}] = \imath \omega \mathcal{F}[\frac{1}{1+t^{2}}]</tex> <tex>\mathcal{F}[\frac{2t}{(1+t^{2})^{2}}] = \imath \omega \mathcal{F}[\frac{1}{1+t^{2}}]</tex>](lib/plugins/latex/images/0149b362e37f4e3a3f1d97b65d5e0dffa9b6e793_0.png)
⇒ ![<tex>\mathcal{F}[\frac{t}{(1+t^{2})^{2}}] = \frac{\imath \omega \pi}{2}e^{-|x|}</tex> <tex>\mathcal{F}[\frac{t}{(1+t^{2})^{2}}] = \frac{\imath \omega \pi}{2}e^{-|x|}</tex>](lib/plugins/latex/images/dee153b749f5c9db378e53abdb2bd768846c2a63_0.png) .
.
Punto V
a)
Primero hay que notar que 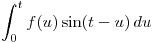 es el producto de convolución entre
es el producto de convolución entre  y
y 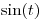 .
.
Entonces se puede aplicar la transformada de Laplace a cada término de la expresión 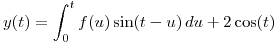 quedando:
quedando:
![<tex>\mathcal{L}[y(t)] = \mathcal{L}[f(t)]\mathcal{L}[\sin(t)] + 2\mathcal{L}[\cos(t)]</tex> <tex>\mathcal{L}[y(t)] = \mathcal{L}[f(t)]\mathcal{L}[\sin(t)] + 2\mathcal{L}[\cos(t)]</tex>](lib/plugins/latex/images/68f4e5d97d7ba56c290a10e0aaad0a679596e601_0.png)
![<tex>\mathcal{L}[\sin(t)] = \frac{1}{1 + s^{2}}</tex> <tex>\mathcal{L}[\sin(t)] = \frac{1}{1 + s^{2}}</tex>](lib/plugins/latex/images/9833711c966a81cdf7025c599ed869a9d1530d36_0.png)
![<tex>\mathcal{L}[\cos(t)] = \frac{s}{1 + s^{2}}</tex> <tex>\mathcal{L}[\cos(t)] = \frac{s}{1 + s^{2}}</tex>](lib/plugins/latex/images/83533d87d78bf652c31c354b2e766cc5fee80b99_0.png)
![<tex>\mathcal{L}[y(t)] = \mathcal{L}[f(t)]\frac{1}{1 + s^{2}} + 2\frac{s}{1 + s^{2}}</tex> <tex>\mathcal{L}[y(t)] = \mathcal{L}[f(t)]\frac{1}{1 + s^{2}} + 2\frac{s}{1 + s^{2}}</tex>](lib/plugins/latex/images/d48782feafc0fa36dd4f859949ad7f571cdd4d76_0.png)
Despejo ![<tex>\mathcal{L}[f(t)]</tex> <tex>\mathcal{L}[f(t)]</tex>](lib/plugins/latex/images/fac52f2440105201ac36c8f097c5f3c508e06078_0.png) :
:
 - 2s = \mathcal{L}[f(t)]</tex> <tex>\mathcal{L}[y(t)](1+s^{2}) - 2s = \mathcal{L}[f(t)]</tex>](lib/plugins/latex/images/2d7e1a89fd3d9b7572d8111160d7738ba2180a9d_0.png)
![<tex>s^{2}\mathcal{L}[y(t)] - s2 - s0 + \mathcal{L}[y(t)] = \mathcal{L}[f(t)]</tex> <tex>s^{2}\mathcal{L}[y(t)] - s2 - s0 + \mathcal{L}[y(t)] = \mathcal{L}[f(t)]</tex>](lib/plugins/latex/images/d3b27c524563825eb8e3ad76b260c5293be6ee6f_0.png)
Antitransformo:
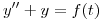 ,
, 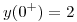 y
y 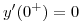 .
.
b)
c) La función 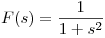 es la transformada de Laplace de
es la transformada de Laplace de 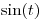
Calculando los límites por separado se puede ver que no coinciden:
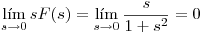
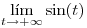 no existe porque la función seno oscila.
no existe porque la función seno oscila.
Que los limites no coincidan muestra que no se puede aplicar el teorema. Esto pasa porque 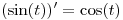 no converge, y una condición necesaria es que
no converge, y una condición necesaria es que 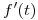 tenga abscisa de convergencia negativa.
tenga abscisa de convergencia negativa.

![<tex>\mathcal{F}[\hat f (\omega)] = 2 \pi f(-t)</tex> <tex>\mathcal{F}[\hat f (\omega)] = 2 \pi f(-t)</tex>](lib/plugins/latex/images/750b8075cbb3d055efd8fb1d07012b61d3190b44_0.png)
![<tex>\mathcal{F}[f'(t)] = \imath \omega \hat f (\omega) </tex> <tex>\mathcal{F}[f'(t)] = \imath \omega \hat f (\omega) </tex>](lib/plugins/latex/images/81a06d5db0498cde7ebfbcd2f0f7e2682bfff0f3_0.png)
![<tex>\mathcal{F}[f(t-a)] = e^{- \imath \omega a}\hat f (\omega)</tex> <tex>\mathcal{F}[f(t-a)] = e^{- \imath \omega a}\hat f (\omega)</tex>](lib/plugins/latex/images/dfa40f35e48c80a568096a2d50fd22baed71d5cb_0.png)


