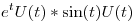Examen Final - 61.10. Analisis Matemático IIIA
Cátedra: Isaacson
Día: 24/02/2009
Enunciado
Punto I
Sea 
una curva simple cerrada orientada positivamente. Hallar los valores de 
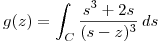cuando 
es interior a y cuando es exterior a . Justificar claramente.
Punto II
a)
Sea 
regular a trozos y periódica de período 
. Si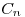 
son los coeficientes de la serie exponencial de Fourier de , hallar los coeficientes de la serie exponencial de Fourier de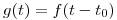 
. ¿Cambia la magnitud de los coeficientes de Fourier al desplazar la función periódica en el tiempo?
b)
Explicar si para las siguientes funciones sus series de Fourier convergen en media, puntualmente o uniformemente. Determinar si se pueden derivar las series y, en caso afirmativo, la función a la cual convergen las series derivadas en ![<tex>[-\pi , \pi]</tex>](lib/plugins/latex/images/5bf4fd74aff4f50d827b6a8b2c25208709fa7b0f_0.png "<tex>[-\pi , \pi]</tex>")
. (No calcular las series)
i)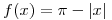 
![<tex>x\in[-\pi , \pi]</tex>](lib/plugins/latex/images/c21bc11503fc63f220812bae248a07c709f29da1_0.png "<tex>x\in[-\pi , \pi]</tex>")
ii)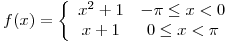 
Punto III
a)
Determinar sabiendo que:
i) es real y no negativa
ii)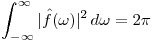 
iii) ![<tex>\mathcal{F}^{-1}[(1 + \imath \omega )] = Ae^{-2t}</tex>](lib/plugins/latex/images/033d0632fed9f28507ac89bd2067fe9e01dd10e6_0.png "<tex>\mathcal{F}^{-1}[(1 + \imath \omega )] = Ae^{-2t}</tex>")
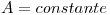
b)
Sea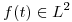 
y continua a trozos. Hallar la transformada de Fourier de 
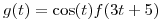en función de 
.
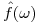Punto IV
a)
Definir producto de convolución: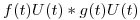 
, estableciendo condiciones suficientes para su existencia.
b)
Demostrar que ![<tex>\mathcal{L}[f(t)U(t) \ast g(t)U(t)] = F(s).G(s)</tex>](lib/plugins/latex/images/0ebdb49d9b7e1519e9ddece237a3d7422778fd39_0.png "<tex>\mathcal{L}[f(t)U(t) \ast g(t)U(t)] = F(s).G(s)</tex>")
c)
Calcular: 
