Tabla de Contenidos
Examen Final - 61.10. Analisis Matemático IIIA
Cátedra: Isaacson
Día: 17/02/2009
Enunciado
Punto I
Hallar 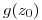 si
si 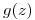 es entera,
es entera,  holomorfa salvo en
holomorfa salvo en 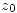 donde tiene un polo de orden
donde tiene un polo de orden  y
y 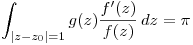 . Justificar claramente todos los pasos.
. Justificar claramente todos los pasos.
Punto II
a
Hallar el desarrollo en Serie de Fourier de senos de 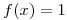 ,
, 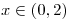 por derivación del desarrollo en Serie de Fourier de una función adecuada, justificando por qué dicha derivación es posible.
por derivación del desarrollo en Serie de Fourier de una función adecuada, justificando por qué dicha derivación es posible.
b
Hallar, si es posible, a partir de a): 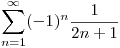
Punto III
a
Si  = \frac{1}{w^2 +1}</tex> <tex>\mathcal{F}[f(t)](w) = \frac{1}{w^2 +1}</tex>](lib/plugins/latex/images/6ad7e0b157fb2f27ee1754f13c4fa614d0ead04b_0.png) , sin antitransformar hallar la Transformada de Fourier de
, sin antitransformar hallar la Transformada de Fourier de 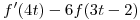 enunciando las hipotesis necesarias.
enunciando las hipotesis necesarias.
b
Hallar  y
y  tales que:
tales que:
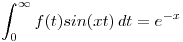 ,
, 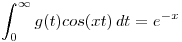 ,
, 
Punto IV
a
Hallar ![<tex>\mathcal{L}[f^{(n)}(t-a)U(t-a)]</tex> <tex>\mathcal{L}[f^{(n)}(t-a)U(t-a)]</tex>](lib/plugins/latex/images/c7b11b1a5666997c322803fe15ecf8b34274fb8b_0.png)
b
Resolver:
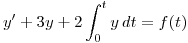 ,
, 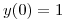 , siendo
, siendo 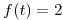 si
si 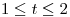 ,
, 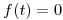 si
si 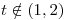
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
