Análisis Matemático III - Curso Ing. Murmis
2007 - 1er cuatrimestre - Evaluación integradora - 4ta oportunidad (06/08/07)
- P1)

- Encontrar la serie de Laurent de
 .
. - Calcular el
 y
y 
- Calcular

- P2) Resolver
 en
en 
- P3) Hallar la antitransformada de Fourier de

- T1) Demostrar
 ⇒
⇒ 
- T2) Demostrar que la sucesión
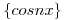 ;
; 

![<tex>[-\pi, \pi]</tex> <tex>[-\pi, \pi]</tex>](lib/plugins/latex/images/5eb4294fac02194086e5b291555e9263269ebc39_0.png) ;
;  es ortogonal pero no completa en el espacio de las funciones continuas
es ortogonal pero no completa en el espacio de las funciones continuas ![<tex>[-\pi, \pi]</tex> <tex>[-\pi, \pi]</tex>](lib/plugins/latex/images/5eb4294fac02194086e5b291555e9263269ebc39_0.png) .
. - T3) Analizar la transformación
 . ¿Es conforme?.
. ¿Es conforme?. - T4) Hallar la antitransformada de Laplace de
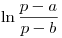
- T5) Calcular
 (Ayuda: usar
(Ayuda: usar ![<tex>\mathbf L[J_o(t)] = \frac{1}{\sqrt{p^2+1}}</tex> <tex>\mathbf L[J_o(t)] = \frac{1}{\sqrt{p^2+1}}</tex>](lib/plugins/latex/images/866fe486afe90fcae1624d9b501582f0f9f38ef1_0.png) )
)
Nota: Se aprobaba con por lo menos 2 Prácticos y 3 Teóricos.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
