Tabla de Contenidos
Integrador 28/02/2006 - Cátedra Isaacson
Enunciado
- Sea
 real y par, periódica de período
real y par, periódica de período 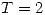 y
y 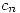 sus coeficientes complejos de Fourier.
sus coeficientes complejos de Fourier.- Demostrar que
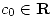 y
y 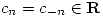 .
. - Hallar
 si además se sabe que
si además se sabe que 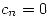 si
si 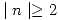 ,
, 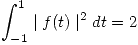 y
y 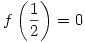
- Dada la ecuación:
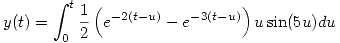 ,
,- Hallar
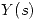 y graficar la región de convergencia.
y graficar la región de convergencia. - Hallar la ecuación diferencial y las condiciones iniciales del problema cuya solución es
 .
.
- Demostrar que si
![<tex>\mathcal{F} \left[ f(t) \right] = \widehat f (\omega) </tex> <tex>\mathcal{F} \left[ f(t) \right] = \widehat f (\omega) </tex>](lib/plugins/latex/images/72b50fde4ab91319388d3f527be4553b4b682130_0.png) , entonces
, entonces ![<tex>\mathcal{F} \left[ f(t) \sin (bt) \right] = \frac{1}{2i} \left[ \widehat f (\omega -b) - \widehat f (\omega +b) \right] </tex> <tex>\mathcal{F} \left[ f(t) \sin (bt) \right] = \frac{1}{2i} \left[ \widehat f (\omega -b) - \widehat f (\omega +b) \right] </tex>](lib/plugins/latex/images/f1c4826123c7f1d67a5116a7a7a6f0637eaf717c_0.png) .
. - Utilizar a) y una propiedad adecuada para hallar
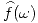 , siendo
, siendo ![<tex>f(t) = \frac{\sin (bt)}{a^2 + t^2} \mbox{ y } \mathcal{F} \left[ e^{-a \mid t \mid } \right] = \frac{2a}{a^2 + \omega^2}</tex> <tex>f(t) = \frac{\sin (bt)}{a^2 + t^2} \mbox{ y } \mathcal{F} \left[ e^{-a \mid t \mid } \right] = \frac{2a}{a^2 + \omega^2}</tex>](lib/plugins/latex/images/757acf52ae4c0177e307b9b5267a2ee553045efb_0.png)
- Hallar
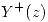 , su región de convergencia y la sucesión
, su región de convergencia y la sucesión 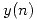 sabiendo que:
sabiendo que:
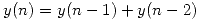 ,
, 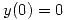 ,
, 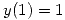 .
.
Resolución
- La Serie Compleja de Fourier de
 es
es 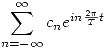 con
con 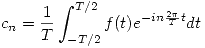
- Por la identidad de Euler, tenemos que
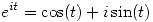
- Entonces nos queda:
![<tex>c_n = \frac{1}{T} \int_{-T/2}^{T/2} f(t) \left[ \cos \left( n \frac{2 \pi}{T} t \right) - i \sin \left( n \frac{2 \pi}{T} t \right) \right] dt</tex> <tex>c_n = \frac{1}{T} \int_{-T/2}^{T/2} f(t) \left[ \cos \left( n \frac{2 \pi}{T} t \right) - i \sin \left( n \frac{2 \pi}{T} t \right) \right] dt</tex>](lib/plugins/latex/images/36990659693894b0947b5ce944f5d024e9bf53a2_0.png)
- Aplicando propiedad distributiva y linealidad de la integral:
![<tex>c_n = \frac{1}{T} \left[ \int_{-T/2}^{T/2} f(t) \cos \left( n \frac{2 \pi}{T} t \right) dt - i \int_{-T/2}^{T/2} f(t) \sin \left( n \frac{2 \pi}{T} t \right) dt \right]</tex> <tex>c_n = \frac{1}{T} \left[ \int_{-T/2}^{T/2} f(t) \cos \left( n \frac{2 \pi}{T} t \right) dt - i \int_{-T/2}^{T/2} f(t) \sin \left( n \frac{2 \pi}{T} t \right) dt \right]</tex>](lib/plugins/latex/images/85790ba6fede93fd343b0b41fe916710b56d9fa9_0.png)
- Como
 y
y 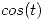 son funciones pares, y
son funciones pares, y 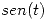 es una función impar, tenemos lo siguiente:
es una función impar, tenemos lo siguiente:
El producto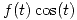 será una función par.
será una función par.
El producto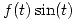 será una función impar.
será una función impar.
La integral de una función impar, en un intervalo de la forma![<tex> \left[ \-a \mbox{;} a \right]</tex> <tex> \left[ \-a \mbox{;} a \right]</tex>](lib/plugins/latex/images/4fda2848df357a442c30f70711c84b2b9ff7b62a_0.png) será nula.
será nula. - Entonces el segundo miembro se anula, y nos queda:
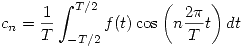
- Al ser
 una función real, la integral anterior también será real. Por lo tanto
una función real, la integral anterior también será real. Por lo tanto 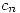 es real y en particular
es real y en particular 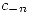 y
y 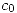 tambien lo serán.
tambien lo serán.
Como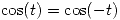 , evidentemente
, evidentemente  .
. - Tenemos lo siguiente:
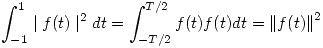
- También sabemos, por la Identidad de Parseval:
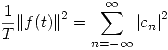
- Entonces:
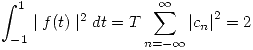
- Sabiendo que
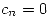 si
si 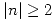 y
y 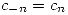 , nos quedan las siguientes igualdades:
, nos quedan las siguientes igualdades:
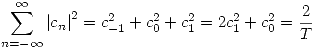
y
![<tex>f(t) = c_{-1}e^{- i \frac{2 \pi}{T} t} + c_{0} + c_{1}e^{i \frac{2 \pi}{T} t} = c_0 + c_{1} \left[ e^{i \frac{2 \pi}{T} t} + e^{- i \frac{2 \pi}{T} t} \right] = c_0 + 2 c_1 \cos \left( \frac{2 \pi}{T} t \right) </tex> <tex>f(t) = c_{-1}e^{- i \frac{2 \pi}{T} t} + c_{0} + c_{1}e^{i \frac{2 \pi}{T} t} = c_0 + c_{1} \left[ e^{i \frac{2 \pi}{T} t} + e^{- i \frac{2 \pi}{T} t} \right] = c_0 + 2 c_1 \cos \left( \frac{2 \pi}{T} t \right) </tex>](lib/plugins/latex/images/0ed7fa09b10c40eaab9001e5cd45c4783c17c1d9_0.png)
- Con el dato
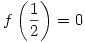 , podemos encontrar el valor de
, podemos encontrar el valor de 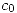 :
:
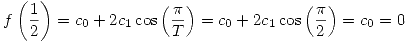
- Reemplazando
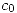 en la otra ecuación:
en la otra ecuación:
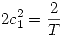
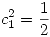
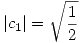
- Concluyendo, tenemos las siguientes dos soluciones para
 :
:
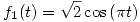
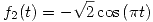
- Gráficos de las funciones:
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

