Examen Final - 61.10. Analisis Matemático IIIA
Cátedra: Isaacson
Día: 08/07/2003
Enunciado
Punto I
Siendo 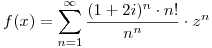 hallar el radio de convergencia r y calcular
hallar el radio de convergencia r y calcular 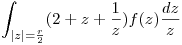
Punto II
Sea  real y par, periódica de período
real y par, periódica de período  Sus coeficientes de Fourier
Sus coeficientes de Fourier 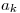 verifican:
verifican:  , si
, si  Si se cumple que:
Si se cumple que: 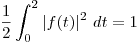 y si
y si 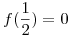 , hallar
, hallar  usando la serie exponencial.
usando la serie exponencial.
Punto III
Si se verifica que 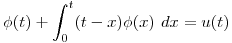 , demostrar que
, demostrar que 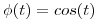
Punto IV
Resolver:
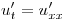
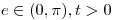
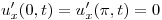
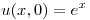
Punto V
Si 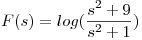 , hallar
, hallar 
Resolución
Punto I
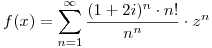
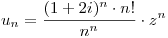
Encuentro el radio de convergencia por Dalambert:
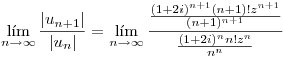
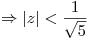
Escribo los primeros terminos de 
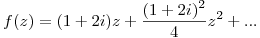
Resolvemos la integral:
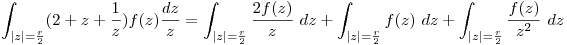
Resuelvo con la formula integral de Cauchy.
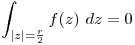
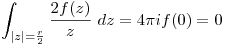
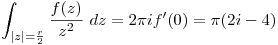
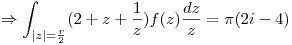
Punto II
Planteo la identidad de Parseval:
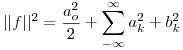
Como la función es par 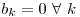
Y segun el dato del enunciado:  si
si 
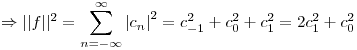
El otro dato del enunciado es:
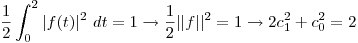
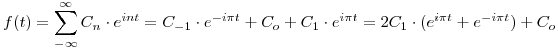
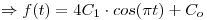
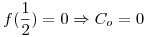
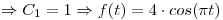
Punto III
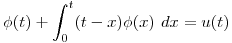
Aplico la transformada de Laplace:
![<tex>\mathcal{L} [\phi(t)] + \mathcal{L} [\int_0^t (t-x) \phi(x) \ dx] = \mathcal{L} [u(t)]</tex> <tex>\mathcal{L} [\phi(t)] + \mathcal{L} [\int_0^t (t-x) \phi(x) \ dx] = \mathcal{L} [u(t)]</tex>](lib/plugins/latex/images/682f3f8668ec4aa03970c2b6226cc65a81148bf5_0.png)
Por propiedades del producto convolución:
![<tex>\mathcal{L} [\phi(t)] + \mathcal{L} [t] \cdot \mathcal [\phi(x)] = \mathcal{L} [u(t)] </tex> <tex>\mathcal{L} [\phi(t)] + \mathcal{L} [t] \cdot \mathcal [\phi(x)] = \mathcal{L} [u(t)] </tex>](lib/plugins/latex/images/97374bb40028b4e87a59bf22188fb799d18d2ed4_0.png)
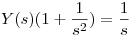
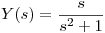
Aplico la antitransformada:
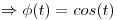
Punto IV
Resuelvo por separación de variables:
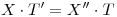
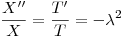
Me quedan dos ecuaciones diferenciales ordinarias:
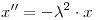 y
y 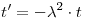
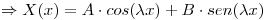
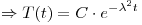
Uso las condiciones iniciales:
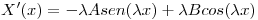
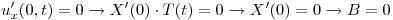
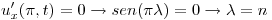
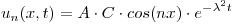
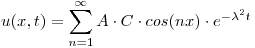
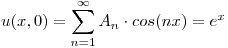
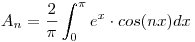
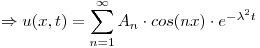
Punto V
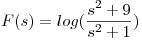
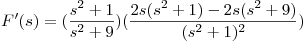
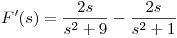
uso la propiedad: ![<tex>\mathcal{L} [t \cdot f(t)] = - F'(s) </tex> <tex>\mathcal{L} [t \cdot f(t)] = - F'(s) </tex>](lib/plugins/latex/images/7833a2215f8f57d9ab70a7d548ca6cd9b8dbb38d_0.png)
![<tex>\Rightarrow \mathcal{L}^{-1}[F'(s)] = -t \cdot f(t) </tex> <tex>\Rightarrow \mathcal{L}^{-1}[F'(s)] = -t \cdot f(t) </tex>](lib/plugins/latex/images/b502626d3732433aaa462fb6432ad493db6616e0_0.png)