Análisis Matemático III - Curso Ing. Murmis
2001 - 2do cuatrimestre - Evaluación integradora - 3a oportunidad
- P1) Calcular
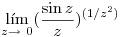
- P2) Resolver
![<tex> \left. \begin{array}{ll} u_{xx} = u_{t} \\ x \in [0,1] \end{array} \right.</tex> <tex> \left. \begin{array}{ll} u_{xx} = u_{t} \\ x \in [0,1] \end{array} \right.</tex>](lib/plugins/latex/images/09af5c8ebf8fd5976a9eb2a8eb462e49c7ca99f5_0.png)
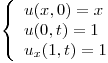
- P3) Dada
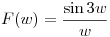 hallar su antitransformada de Fourier
hallar su antitransformada de Fourier  y representarla gráficamente.
y representarla gráficamente. - T1) Analizar cuántos resultados distintos tiene la integral
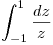 y calcularlos.
y calcularlos. - T2) Demostrar
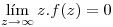 ⇒
⇒ ![<tex> \left\{ \begin{array}{cc} \lim_{R\rightarrow\infty} \oint_{\Gamma_R}f(z)dz = 0\\ \Gamma_R: z = Re^{i\phi} ; \phi \in (0,2\pi] \\\end{array} \right. </tex> <tex> \left\{ \begin{array}{cc} \lim_{R\rightarrow\infty} \oint_{\Gamma_R}f(z)dz = 0\\ \Gamma_R: z = Re^{i\phi} ; \phi \in (0,2\pi] \\\end{array} \right. </tex>](lib/plugins/latex/images/2f294ab6a95721205873df7d196f22d49ae89be8_0.png)
- T3) Demostrar:

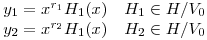
 p(x) tiene a lo sumo polo de
p(x) tiene a lo sumo polo de  orden en 0.
orden en 0.
- q(x) tiene a lo sumo polo de
 orden en 0.
orden en 0.
- T4) A partir de
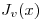 probar que
probar que 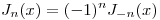
- T5) Calcular
 (Ayuda: usar
(Ayuda: usar ![<tex>\mathbf L[J_o(t)] = \frac{1}{\sqrt{p^2+1}}</tex> <tex>\mathbf L[J_o(t)] = \frac{1}{\sqrt{p^2+1}}</tex>](lib/plugins/latex/images/866fe486afe90fcae1624d9b501582f0f9f38ef1_0.png) )
)
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
