Análisis Matemático III - Curso Ing. Murmis
2001 - 1er cuatrimestre - Evaluación integradora - 2a oportunidad
- P1) Calcular el valor principal de
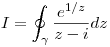
- P2) Resolver
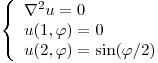
- P3) Resolver:
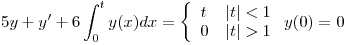
- T1) Analizar cuántos resultados distintos tiene la integral
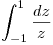 y calcularlos.
y calcularlos. - T2) Demostrar si es verdadero o falso:


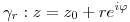 ⇒
⇒ 
![<tex>\varphi \in [0,\alpha]; \alpha < 2\pi</tex> <tex>\varphi \in [0,\alpha]; \alpha < 2\pi</tex>](lib/plugins/latex/images/d75e331cd82f7cae5c9cbfcf1ca7bab0cf87f2e0_0.png)
- T3) Demostrar que la sucesión
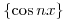 ;
; 

![<tex>[-\pi, \pi]</tex> <tex>[-\pi, \pi]</tex>](lib/plugins/latex/images/5eb4294fac02194086e5b291555e9263269ebc39_0.png) ;
;  es ortogonal pero no completa en el espacio de las funciones continuas
es ortogonal pero no completa en el espacio de las funciones continuas ![<tex>[-\pi, \pi]</tex> <tex>[-\pi, \pi]</tex>](lib/plugins/latex/images/5eb4294fac02194086e5b291555e9263269ebc39_0.png) .
. - T4) Demostrar:


 p(x) tiene a lo sumo polo de
p(x) tiene a lo sumo polo de  orden en 0.
orden en 0.
- q(x) tiene a lo sumo polo de
 orden en 0.
orden en 0.
- T5) Demostrar los teoremas del desplazamiento de la original y del desplazamiento de la transformada de Laplace.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


