Análisis Matemático III - Curso Ing. Murmis
2001 - 1er cuatrimestre - Evaluación integradora - 1a oportunidad
- P1) Calcular
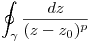
![<tex>\gamma: \left. \begin{array}{cc} z = z_0 + re^{it} \\ t \in [0;2\pi] \\\end{array} \right. </tex> <tex>\gamma: \left. \begin{array}{cc} z = z_0 + re^{it} \\ t \in [0;2\pi] \\\end{array} \right. </tex>](lib/plugins/latex/images/2cb4f4c5298667a2ff550c5044565be2e3720920_0.png)
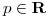
- P2) Resolver
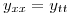
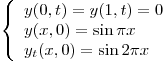
![<tex>x \in [0,1]</tex> <tex>x \in [0,1]</tex>](lib/plugins/latex/images/25b3e8f265165db5e67348a8f921f50a1b40f78a_0.png)
- P3) Dada
 hallar su antitransformada de Fourier
hallar su antitransformada de Fourier 
- T1) Demostrar
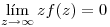 ⇒
⇒ ![<tex> \left. \begin{array}{cc} \lim_{R\rightarrow\infty} \oint_{\Gamma_R}f(z)dz = 0\\ \Gamma_R: z = Re^{i\phi} ; \phi \in (0,2\pi] \\\end{array} \right. </tex> <tex> \left. \begin{array}{cc} \lim_{R\rightarrow\infty} \oint_{\Gamma_R}f(z)dz = 0\\ \Gamma_R: z = Re^{i\phi} ; \phi \in (0,2\pi] \\\end{array} \right. </tex>](lib/plugins/latex/images/074a69221d162a0a9d5f6c6ae8cfa217385980bc_0.png)
- T2) Analizar si
 es punto de ramificación de
es punto de ramificación de 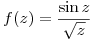
- T3) A partir de
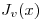 probar que
probar que 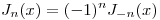
- T4) Demostrar que la antitransformada de Fourier de
![<tex>F(w)=\frac{1}{2\pi}[\frac{1}{iw}+\pi \delta (w)]</tex> <tex>F(w)=\frac{1}{2\pi}[\frac{1}{iw}+\pi \delta (w)]</tex>](lib/plugins/latex/images/0d5fcd2cd2e355b74cf48d068051bd5abfaf2267_0.png) es
es 
- T5) Probar que
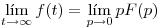 usando la expresión
usando la expresión ![<tex>\mathbf L[f'(t)]</tex> <tex>\mathbf L[f'(t)]</tex>](lib/plugins/latex/images/9e6ec24b7bcc0d253920e556351d2d9fc1b397bd_0.png)
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
