Análisis Matemático III - Curso Ing. Murmis
2001 - 1er cuatrimestre - Evaluación integradora - 4a oportunidad
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


![<tex> \left. \begin{array}{ll} u_{t} = u_{xx} \\ x \in [0,\pi] \\ t \in [0, \infty]\end{array} \right.</tex> <tex> \left. \begin{array}{ll} u_{t} = u_{xx} \\ x \in [0,\pi] \\ t \in [0, \infty]\end{array} \right.</tex>](lib/plugins/latex/images/474318ffbbbc04dc9da44d9589c9514341ebc1a3_0.png)


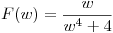 hallar su antitransformada de Fourier
hallar su antitransformada de Fourier  .
.


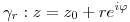 ⇒
⇒ 
![<tex>\varphi \in [0,\alpha]; \alpha < 2\pi</tex> <tex>\varphi \in [0,\alpha]; \alpha < 2\pi</tex>](lib/plugins/latex/images/d75e331cd82f7cae5c9cbfcf1ca7bab0cf87f2e0_0.png)

 ⇒
⇒ 
![<tex>\mathcal{L}[\ln t]=\frac{ \Gamma '(1)-\ln p}{p}</tex> <tex>\mathcal{L}[\ln t]=\frac{ \Gamma '(1)-\ln p}{p}</tex>](lib/plugins/latex/images/e753737733db2c5e400808fac362852b6155fcef_0.png)