Análisis Matemático III - Curso Ing. Murmis
2001 - 1er cuatrimestre - Evaluación integradora - 4a oportunidad
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

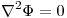 en D y determinar la temperatura
en D y determinar la temperatura 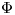 en el punto
en el punto 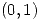

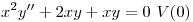
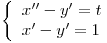
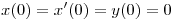
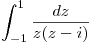 y calcularlos.
y calcularlos.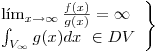 ⇒
⇒ 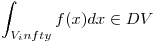
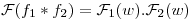
![<tex> \mathcal{L}[J_1(t)] = 1 - \frac{p}{\sqrt{p^2+1}}</tex> <tex> \mathcal{L}[J_1(t)] = 1 - \frac{p}{\sqrt{p^2+1}}</tex>](lib/plugins/latex/images/0a5f9d76d41d31f6af46ccbfda6ff1f52c4ce42d_0.png)
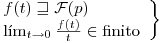 ⇒
⇒