Análisis Matemático III - Curso Ing. Murmis
2000 - 2d0 cuatrimestre - Evaluación integradora - 3a oportunidad - 19/02/2001
- P1) Resolver
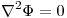 en D.
en D.
- P2) Resolver
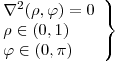
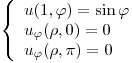
- P3) Dada
 hallar su antitransformada de Fourier
hallar su antitransformada de Fourier 
- T1) Analizar si
 es punto de ramificación de
es punto de ramificación de 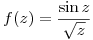
- T2) Analizar cuantos resultados distintos tiene la integral
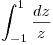 y calcularlos.
y calcularlos. - T3) Demostrar:


 p(x) tiene a lo sumo polo de
p(x) tiene a lo sumo polo de  orden en 0.
orden en 0.
- q(x) tiene a lo sumo polo de
 orden en 0.
orden en 0.
- T4) Obtener las fórmulas de la serie exponencial de Fourier y sus coeficientes a partir de las fórmulas de la serie trigonométrica de Fourier.
- T5) Hallar la antitransformada de Laplace de
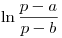
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported


