Análisis Matemático III - Curso Ing. Murmis
2000 - 2d0 cuatrimestre - Evaluación integradora - 3a oportunidad - 31/07/2000
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

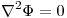 en D.
en D.
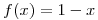 ;
; ![<tex>x \in [0,1]</tex> <tex>x \in [0,1]</tex>](lib/plugins/latex/images/25b3e8f265165db5e67348a8f921f50a1b40f78a_0.png) en serie de Fourier como función par.
en serie de Fourier como función par.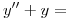
![<tex> \left\{ \begin{array}{ll}\sin t & t \in [0, \pi]\\0 & t > \pi\\\end{array} \right. </tex> <tex> \left\{ \begin{array}{ll}\sin t & t \in [0, \pi]\\0 & t > \pi\\\end{array} \right. </tex>](lib/plugins/latex/images/7fdb8e2086d3475bda17cb5551dac953dea7eec5_0.png) ;
; 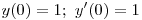
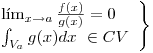 ⇒
⇒ 
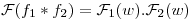
 ⇒
⇒ 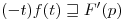 .
. 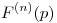
 (Ayuda: usar
(Ayuda: usar ![<tex>\mathcal{L}[J_o(t)] = \frac{1}{\sqrt{p^2+1}}</tex> <tex>\mathcal{L}[J_o(t)] = \frac{1}{\sqrt{p^2+1}}</tex>](lib/plugins/latex/images/46c0072aba97247879dbf321a76a7e7ba8c2ebf8_0.png) )
)