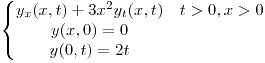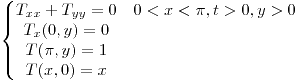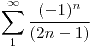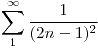Examen Final - 61.10. Análisis Matemático III - 14/02/2013
- Enunciado
  - Punto I
  - Punto II
  - Punto III
  - Punto IV
  - Punto V
- Resolución
- Discusión

2013

Cátedra: Todas
Fecha: Cuarta Oportunidad - Verano 2013
Día: 14/02/2013

Esta página está incompleta; podés ayudar completando el material.

Enunciado

Es común que haya errores en el enunciado, los cuales son aclarados (o no) inoportunamente en la mitad del examen; si ves algo que te parece que está mal, posiblemente lo esté (pero no te confíes).

En el primer cuadrante fluye el calor en régimen permanente, permaneciendo el eje $<tex>y</tex>$ a temperatura $<tex>0^{\circ}C</tex>$ . Proponga una condición de contorno sobre el eje x de modo que se pueda hallar la distribución de temperaturas en dicha región:

Utilizando la transformada seno de Fourier.
Utilizando transformación conforme.
Con la funciones propuestas resuelva dichos problemas.

Punto II

Estableciendo hipótesis necesarias, enuncie y demuestre la propiedad que permite obtener la transformada de Laplace de la función integral de una función $<tex>f(t)</tex>$ en función de la transformada de Laplace de $<tex>f(t)</tex>$ .
Utilice la transformada de Laplace para resolver:
1. $<tex>\left \lbrace \begin{matrix} y_x(x,t) + 3x^2 y_t(x,t) & t> 0, x> 0 \\y(x,0) = 0&\\y(0,t)=2t&\end{matrix} \right .</tex>$

Punto III

Resuelva el siguiente problema de contorno:

$<tex>\left \lbrace \begin{matrix} T_{xx} + T_{yy} = 0 & 0<x <\pi, t >0, y > 0\\T_x(0,y)=0&\\T(\pi, y)=1&\\T(x,0)=x\end{matrix} \right .</tex>$

Punto IV

Enuncie el teorema de la fórmula integral de Cauchy y explique cómo lo extiende a una región $<tex>D</tex>$ doblemente conexa limitada exteriormente e interiormente por las curvas simples cerradas $<tex>\Gamma_1</tex>$ y $<tex>\Gamma_2</tex>$ , respectivamente.
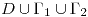Sean las curvas simples cerradas $<tex>\Gamma_1</tex>$ y $<tex>\Gamma_2</tex>$ que limitan exteriormente e interiormente, respectivamente, la región $<tex>D</tex>$ del plano complejo. $<tex>f(z)</tex>$ es una función holomorfa en $<tex>D \cup \Gamma_1 \cup \Gamma_2</tex>$ . Los puntos 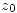$<tex>z_0</tex>$ y $<tex>z_1</tex>$ pertenecen a $<tex>D</tex>$ . Se sabe que: $<tex>\frac{1}{2\pi i} \left[ \oint_{\Gamma_1} \frac{f(z)}{(z-z_0)(z-z_1)}dz - \frac{1}{2 \pi i} \oint_{\Gamma_2} \frac{f(z)}{(z-z_0)(z-z_1)} dz \right]=\frac{8}{z_1-z_0}</tex>$ y que $<tex>4 f(z_1) + f(z_0) = 6</tex>$ , obtenga $<tex>f(z_1)</tex>$ y $<tex>f(z_0)</tex>$ . Enuncie el teorema que aplique y explique cómo lo aplicó.

Punto V

Obtenga el D.S.F de consenos de $<tex>f(x) = \left \lbrace \begin{matrix} 1 & si & 0<x < \pi/2 \\2 & si & \pi/2 < x < \pi \end{matrix} \right.</tex>$
Defina la función $<tex>f^{*}: [0,\pi] \to \mathbf{R}</tex>$ a la cual dicho desarrollo converge puntualmente.
Calcule
1. $<tex>\sum_1^\infty \frac{(-1)^n}{(2n-1)}</tex>$
2. $<tex>\sum_1^\infty \frac{1}{(2n-1)^2}</tex>$

Resolución

Discusión

Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.