Análisis Matemático III
- 2009 - Evaluación integradora - 1ra oportunidad (29/06/09)
  - Enunciado
  - Resolucion

Análisis Matemático III

2009 - Evaluación integradora - 1ra oportunidad (29/06/09)

Enunciado

P1) La función $<tex>m(x,y) = \frac{-y}{x^2+y^2}e^{3x}\cos(3y)+\frac{x}{x^2+y^2}e^{3x}\sin(3y)</tex>$ es la parte imaginaria de la función de variable compleja holomorfa en $<tex>C - \{0\}</tex>$ .
- 1. Halle la parte real $<tex>n(x,y)</tex>$ y la correspondiente función $<tex>f(z)</tex>$ .
- 2. Halle el ángulo que forman las curvas de nivel de $<tex>m(x,y)</tex>$ y las de $<tex>n(x,y)</tex>$ en el punto $<tex>(1,1)</tex>$ .
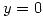- 3. Sean $<tex>\gamma_1</tex>$ y $<tex>\gamma_2</tex>$ las rectas $<tex>x=1</tex>$ y $<tex>y=0</tex>$ respectivamente en el plano complejo $<tex>z</tex>$ , y sean $<tex>\Gamma_1</tex>$ y $<tex>\Gamma_2</tex>$ sus correspondientes imágenes en el plano $<tex>\omega</tex>$ cuando se les aplica la función $<tex>f(z)</tex>$ . Decir que ángulo forman $<tex>\Gamma_1</tex>$ y $<tex>\Gamma_2</tex>$ en el punto $<tex>\left( e^3,0\right)</tex>$ en el plano $<tex>\omega</tex>$ .
P2) Sea $<tex>f(x) = \left\{ \begin{array}{ll}1 & x = 0\\ 10 & x=\pi \\ x & \forall x \ne \pi \ne 0 \\ \end{array} \right.</tex>$ en el intervalo $<tex>[0,2\pi]</tex>$ .
- 1. Haga el desarrollo en serie trigonométrica de Fourier de cosenos de dicha función y explique a que función CV.
- 2. Utilice dicho desarrollo para obtener una serie numérica que converja a $<tex>\int_0^{2\pi}x^2 dx</tex>$
P3) Describa una situación física representada por el siguiente problema, y resuelvalo.

$<tex>\left[ \begin{array}{cl}u_t^{'}(x,t) = u_{xx}^{''}(x,t) & 0\le x \le 2\pi ;\, t>0\\u(0,t)=0 & t>0\\u(2\pi,t)=1 &t>0\\u(x,0) = x & 0\le x \le 2\pi \\ \end{array} \right. </tex>$

P4) Si la $<tex>L(f(t)) = F(s)</tex>$ , hallar $<tex>L \left[t\left( \int_0^{t-a} f(u)du\right) H(t-a)\right]</tex>$ . Demuestre todas las propiedades de la T.L. que haya utilizado.

Análisis Matemático III

2009 - Evaluación integradora - 1ra oportunidad (29/06/09)

Enunciado

Resolucion