Tabla de Contenidos
Análisis Matemático III - Curso Ing. Murmis
2008 - Evaluación integradora - 1ra oportunidad (12/02/08)
Enunciado
- P1) Calcular

- P2) Resolver
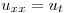 ,
, ![<tex> x \in [0,1] </tex> <tex> x \in [0,1] </tex>](lib/plugins/latex/images/0be24dcbbcc248928b1d8497d347a84e066c35c2_0.png)
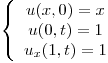
- P3) Resolver
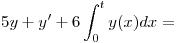
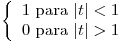
- T1) Analizar
 ⇒
⇒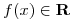
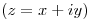
- T2) Demostrar si es V o F:
 ⇒
⇒![<tex> R[f(z);z_{\infty}]=0</tex> <tex> R[f(z);z_{\infty}]=0</tex>](lib/plugins/latex/images/e94c146026680e8e5be56f0763383a19c80ef7bb_0.png)
- T3) Probar que

- T4) Demostrar

- T5) Calcular
![<tex>\mathcal{L}[\ln t]=\frac{ \Gamma '(1)-\ln p}{p}</tex> <tex>\mathcal{L}[\ln t]=\frac{ \Gamma '(1)-\ln p}{p}</tex>](lib/plugins/latex/images/e753737733db2c5e400808fac362852b6155fcef_0.png)
Resolucion
- P1)

Para encontrar 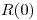 desarollar
desarollar 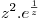 en forma de serie, partiendo de la serie conocida de
en forma de serie, partiendo de la serie conocida de 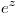 luego de tener bien armada la serie calcular los primeros 4 terminos: SERIE = z^2 + z + 1/2 + 1/(6*z) + …. Lo que importa es que R(0) = 1/6 porque es el numero que acompaña al termino
luego de tener bien armada la serie calcular los primeros 4 terminos: SERIE = z^2 + z + 1/2 + 1/(6*z) + …. Lo que importa es que R(0) = 1/6 porque es el numero que acompaña al termino 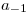 osea a 1/z
osea a 1/z
- P2) Proponer una v(x,t) que cumpla:
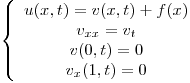
Trabajando con estas ecuaciones y las de u(x,t) se deduce que f(x)= x + 1 Ahora se sigue el ejercicio como todos los otros de la guia, pero en lugar de trabajar con u trabajando con v. Osea, se hace separacion de variables v(x,t) = X(x).T(t) y se sigue………..
- P3) Hay que tomar la transformada de Laplace de ambos lados de la igualdad. Aplicando propiedades etc, etc.
- T1) Yo llegue a que era VERDADERA. Dije esto:
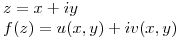
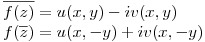 Las iguale y me quedaron estas 2 ecuaciones:
Las iguale y me quedaron estas 2 ecuaciones:
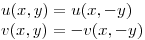
Despues puse y=0 (porque el enunciado hablaba de 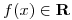 ) y las ecuaciones quedaron asi:
) y las ecuaciones quedaron asi:
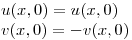 ⇒
⇒ 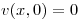 ⇒
⇒ 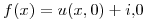 ⇒
⇒ 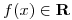
- T2) Es FALSA, contraejemplo
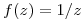
- T3) Resolucion en el apunte de Sacerdotti Transformada de Laplace, pagina 30. El ejercicio pide con Transformada de Fourier y en el apunte esta hecho con la de Laplace pero es practicamente igual (creo).
- T4) Resolucion en el apunte de Sacerdotti Transformada de Laplace, pagina 56. En realidad en el Apunte esta hecho para cualquier
 . En clase hicieron el ejercicio de la guia 9: Anexo\V\a que es muy parecido (en la carpeta de Brumosky esta).
. En clase hicieron el ejercicio de la guia 9: Anexo\V\a que es muy parecido (en la carpeta de Brumosky esta). - T5) Resolucion en el apunte de Sacerdotti Transformada de Laplace, pagina 53.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
