Tabla de Contenidos
Resultados de la Guía - Probabilidad y Estadística (61.06 y 61.09)
Guía 1: Probabilidad
- 0.56
- 0.14
- 0.04
- 0.26
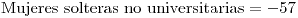
- 0.36
- 0.64
- 0.53
- 0.17
- 0.75
- Roja
- Roja
- Blanca
- 0.45
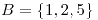
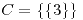
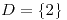 o
o 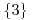 o
o 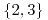 o
o 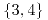 o
o 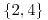 o
o 

- 2/7
- 16/35
- 19/35
- 2/5
- El esposo.
- 1/6
- 13/18
- 1/12
- 1/4
- 5/18
- 0.5
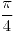
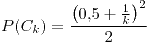 con
con 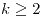 ;
; 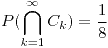
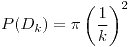 ;
; 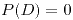
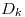 representa el evento de que el dardo caiga dentro del círculo con centro en
representa el evento de que el dardo caiga dentro del círculo con centro en 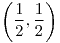 y radio
y radio 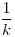 .
.
 representa el evento de que el dardo caiga en el centro del círculo.
representa el evento de que el dardo caiga en el centro del círculo.
- 1/1000
- 1/59049
- 0
- Con reposición:
- 1/64
- 1/16
- 1/1600
- 3/8
- Sin reposición:
- 3/247
- 12/247
- 0
- 100/247
- 0.7015
- 0.0489
- 0.818
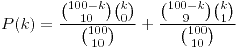 si
si 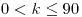
- 0.3329

- 0.916
- Conviene apostar al resultado del evento “A”
- 1/6
- 1/6
- 0
- 1/2
- 1/4
- 0.56
- 5/28
- 8/55
- 17/28
- 7/32
- 1/5
- 60/143
- 5/12
- 12/248
- 12/248
- 0.04858
- 158/63973
- 0.0508
- 1/3
- 1/2
- 3/4
- 1/2
- 3/8
- 1/5
- 0.44
- 19/22
- 9899/9900
- 1/3
- 40/63
- 9/23
- 17/21
- Van a dar los mismos resultados porque las proporciones son las mismas.


- 24/49

- 0.049
- 0.00006734
- 0.049
- 0.000067
- 0.0411
- 0.086

- 0.0611
- Al menos 5 respuestas correctas.
- 0.3671

- 1/2
- No son independientes.

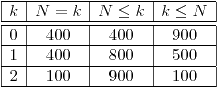

- 17/100
- 1/150
- 1/25
- 23/25
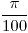

- 1/2
- 1/3

- 1/2
- 1/2

- 4/5

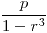 siendo
siendo 

Guía 2: Funciones de densidad, distribución, conjuntas y marginales
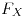 es monótona no decreciente
es monótona no decreciente
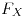 es continua a derecha
es continua a derecha
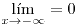
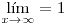
- En
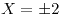 , donde
, donde 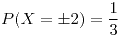
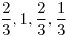
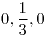
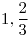
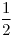

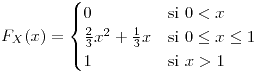
 ,
, 
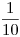

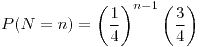 para
para 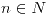
- 4/5
- 3/4
- 2/3
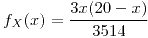 para
para 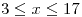
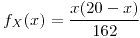 para
para 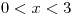 o
o 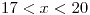
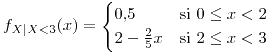
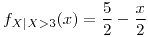 si
si 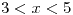
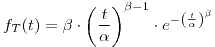
- Fallas casuales.
- Fallas por desgaste.
- Fallas tempranas.
- Fallas tempranas.
- Fallas por desgaste.
- Fallas casuales.

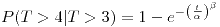
- Sin reposición

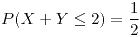
- Con reposición

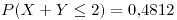
- 1/2
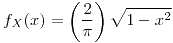 para
para ![<tex>x\in[-1,1]</tex> <tex>x\in[-1,1]</tex>](lib/plugins/latex/images/b9d8f69c2b20d8f881f95c21d8b68a52a6024c71_0.png)
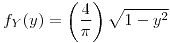 para
para ![<tex>y\in[0,1]</tex> <tex>y\in[0,1]</tex>](lib/plugins/latex/images/aa6234f0415d31fe0e31098a86d7d1f25b0c38e9_0.png)
- No son independientes.
- 5/12
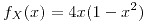 para
para 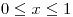
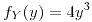 para
para 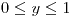
- No son independientes.
- 8/9
- 0.1035
- 4/9
- 0.127
- 1/50
- 47/100
- 17/18
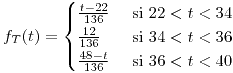
Guía 3: Esperanza, varianza y covarianza
- 1.1


- 1.625
- 2.2
- 2/3
- 1
- 7/9
- 7.2
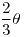
- 19/18
![<tex>E[X|X<1]=\frac{2}{3}</tex> <tex>E[X|X<1]=\frac{2}{3}</tex>](lib/plugins/latex/images/71bd979b218e0813897d1018fe92c149fa82a1cc_0.png)
![<tex>E[X|X\leq1]=\frac{5}{6}</tex> <tex>E[X|X\leq1]=\frac{5}{6}</tex>](lib/plugins/latex/images/17ad086d0a60e6880e047a50443e864c0bcfba10_0.png)
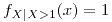 para
para 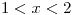
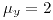




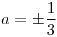 ,
, 
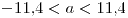
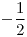
![<tex>E[N]=\frac{19}{9}</tex> <tex>E[N]=\frac{19}{9}</tex>](lib/plugins/latex/images/e05878314b88b60c1dcc8736854d2fab4e6c96ba_0.png)
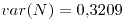
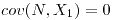

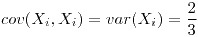 ,
, 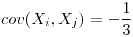
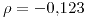

- 1/9
- 2/3
- 2/3
![<tex>E[Z]=\frac{2}{3}</tex> <tex>E[Z]=\frac{2}{3}</tex>](lib/plugins/latex/images/5a02e1cf24a3fcd1b56d42529ada8de08215df0e_0.png) ,
,
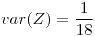
![<tex>E[W]=\frac{1}{3}</tex> <tex>E[W]=\frac{1}{3}</tex>](lib/plugins/latex/images/c38c6bb948aadb66cfe7f78da2e479088f55179e_0.png)
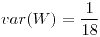
- 7/18
- 1/36
Guía 4: Transformación de variables aleatorias
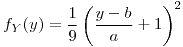 si
si 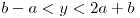
![<tex>f_{Y}(y)=\frac{\left(\sqrt[3]{-y}+1\right)^{2}}{27(-y)^{2/3}}</tex> <tex>f_{Y}(y)=\frac{\left(\sqrt[3]{-y}+1\right)^{2}}{27(-y)^{2/3}}</tex>](lib/plugins/latex/images/6c55db4b972826e550b0d29b75dbe2ee947acdf3_0.png) si
si 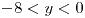 y
y 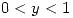
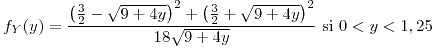
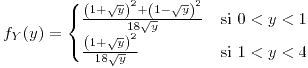
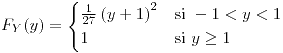
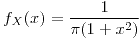 para todo
para todo 

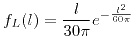 si
si 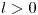
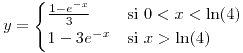
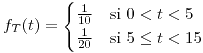
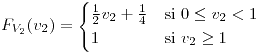
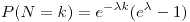 para
para 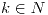
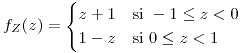
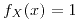 si
si 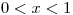
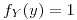 si
si 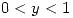
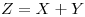
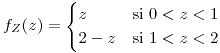
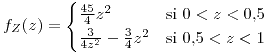

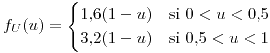
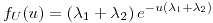 para
para 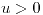
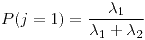
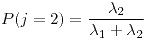

- 0.2314
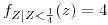 para
para 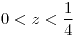


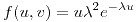 para
para 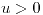 y
y 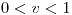
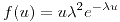 para
para 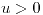
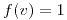 para
para 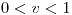
Son independientes.

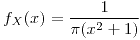 si
si 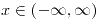

- 0.0128
0.08 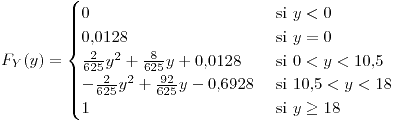
Guía 5: Esperanza y varianza condicional, suma de variables aleatorias, mezcla, truncamiento
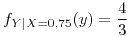 si
si 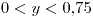
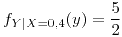 si
si 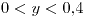
- No son independientes.
 , 0,375
, 0,375
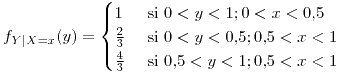
- 0.5

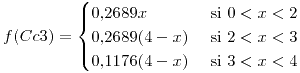
- 0,439
- 0,851
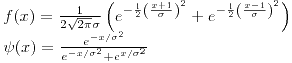
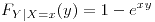 si
si 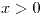 ,
, 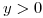
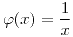 si
si 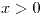
![<tex>E[Y|X]=\frac{1}{X}</tex> <tex>E[Y|X]=\frac{1}{X}</tex>](lib/plugins/latex/images/4714416cafe75028f5c12bdc7dd87efde9f512e7_0.png)
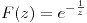 si
si 
- 0,5811
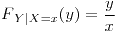 si
si 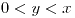 ,
, 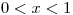
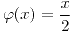 si
si 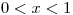
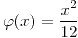 si
si 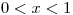
![<tex>E[Y|X]=\frac{X}{2}</tex> <tex>E[Y|X]=\frac{X}{2}</tex>](lib/plugins/latex/images/c63207e1c52efc892955705ecb2ef9cb16a88a7c_0.png)
![<tex>E[Y|X]=\frac{X^{2}}{12}</tex> <tex>E[Y|X]=\frac{X^{2}}{12}</tex>](lib/plugins/latex/images/314edb5990d231160d0e9b1731523643a6811e47_0.png)
 ,
, 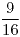
![<tex>Z=E[Y|X]</tex> <tex>Z=E[Y|X]</tex>](lib/plugins/latex/images/77ae03f44904369c49db70b209ae37cce5c43402_0.png)
![<tex>W=var[Y|X]</tex> <tex>W=var[Y|X]</tex>](lib/plugins/latex/images/12069c6397c15bb1238544ab0ff11765ca4e0546_0.png) Z
Z
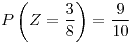
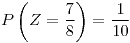
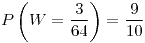
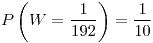
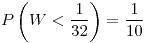
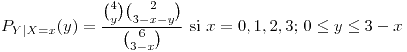 .
.![<tex>E[Y|X=x]=(3-x)\frac{4}{6}</tex> <tex>E[Y|X=x]=(3-x)\frac{4}{6}</tex>](lib/plugins/latex/images/bb8d63a2254d9e7b8872a08dbf8b1cc7aa5ef187_0.png)
![<tex>var[Y|X=x]=\left(9-x^{2}\right)\frac{2}{45}</tex> <tex>var[Y|X=x]=\left(9-x^{2}\right)\frac{2}{45}</tex>](lib/plugins/latex/images/69a1469e96e62f97cece210c9315b96dac8121f9_0.png)
![<tex>E[Y|X]=(3-X)\frac{4}{6}</tex> <tex>E[Y|X]=(3-X)\frac{4}{6}</tex>](lib/plugins/latex/images/49f5c5af9345eba4bdebe00d91eb0d0124fc730f_0.png)
![<tex>V[Y|X]=\left(9-X^{2}\right)\frac{2}{45}</tex> <tex>V[Y|X]=\left(9-X^{2}\right)\frac{2}{45}</tex>](lib/plugins/latex/images/98b665bea22bb0c63b919bd9c3d33dfa796fd21e_0.png)
![<tex>\varphi(x)=E[Y|X]=\frac{e^{x/\sigma^{2}}-e^{-x/\sigma^{2}}}{e^{-x/\sigma^{2}}+e^{x/\sigma^{2}}}</tex> <tex>\varphi(x)=E[Y|X]=\frac{e^{x/\sigma^{2}}-e^{-x/\sigma^{2}}}{e^{-x/\sigma^{2}}+e^{x/\sigma^{2}}}</tex>](lib/plugins/latex/images/6a573c3134679cb203da9158d5af6466e38752ca_0.png)
![<tex>E[Y|X]=0</tex> <tex>E[Y|X]=0</tex>](lib/plugins/latex/images/cbdf433fb1750355db80abd97af2fc4f95da0e33_0.png)
Son independientes.![<tex>E[Y|X]=0</tex> <tex>E[Y|X]=0</tex>](lib/plugins/latex/images/cbdf433fb1750355db80abd97af2fc4f95da0e33_0.png)
No son independientes.
- 14
- 0
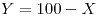
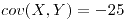
- 2
- 5 mm a la derecha.
- 1
![<tex>E[Y]=7.5</tex> <tex>E[Y]=7.5</tex>](lib/plugins/latex/images/92ff20d2195f682dec50d9885723075c7988fbfc_0.png)
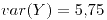
![<tex>E[T]=1.266</tex> <tex>E[T]=1.266</tex>](lib/plugins/latex/images/8b5e49752bba837efd915157a363508ce45a5c3a_0.png)

![<tex>E[Y|X]=\frac{X^{2}}{2}</tex> <tex>E[Y|X]=\frac{X^{2}}{2}</tex>](lib/plugins/latex/images/95044b82a3dfdf34b056cf57f3e9e640ac383176_0.png) si
si 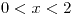
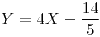

Guía 6: Procesos Bernoulli, geométrico e hipergeométrico
- 0,6241
- 0,6992
- 0,6651
- 0,4018
- 0,2009
- 1 y 2
- 2
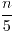
- 0,8233
- 0.05174
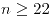
- 0.0531
- 0.2373
![<tex>E[N]=11.4</tex> <tex>E[N]=11.4</tex>](lib/plugins/latex/images/d7c9b9344edb36df689caa4d657a6ac8c11c54ca_0.png)
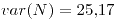
- 40
- 0,03348
- 0,1273

- 0,00277
- 0,1527
- 0,5042
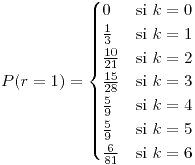
Es más probable cuando o
o  .
.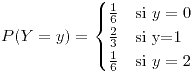
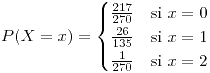
- 19,63%

- 0,1297
- 0,3589
- 0,9896
- 0,2969
- 0,9999
- 0,00065
- 0,303

![<tex>E[M]=1</tex> <tex>E[M]=1</tex>](lib/plugins/latex/images/473414bab1d66a8c9cd635aa7ac212dca0ae2fa9_0.png)
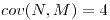
![<tex>E[X]=\frac{1}{9}</tex> <tex>E[X]=\frac{1}{9}</tex>](lib/plugins/latex/images/2cd1b41963a3ddd42960b03477556d79812aab5a_0.png)
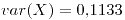
- 7,28
Guía 7: Procesos Poisson
- 0,1429
- 1 y 2
- 1,7817
- 0,218
- Aumento en 1 las instalaciones
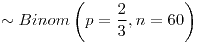
- 0,108
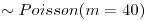
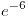
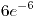
- 1/3
- 0,9901
- Exponencial
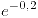
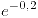
- No tiene memoria
- Gamma
- 0,9999
- 0,6993
![<tex>E[T]=7,692</tex> <tex>E[T]=7,692</tex>](lib/plugins/latex/images/0971d98fa50b10eca555891f030a8dc56feb8cd7_0.png) minutos
minutos- 3/4
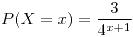 si
si 
- 0,0107
- 0,0286
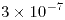
- 1/2
- 5/4
- 0,1025
- 0,2873
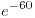
- 1/9
- 5/9
- 0,07985
![<tex>E[T]=2</tex> <tex>E[T]=2</tex>](lib/plugins/latex/images/aced5759f18839b2f8f99897d0301375c868913d_0.png) ,
, 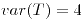
- 16,4
- 0,0656
- 1/4
- 240
- 0
- 0,0148
- 552 Kg
- 331.200 Kg


Guía 8: Distribución normal, TCL
- Trivial.
- Trivial.
- 0,676
- 0,0917
- 243,53
- 491.95
- IC: 394,26; 522,056
- 0.6157

- No son independientes.
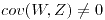
- 0.9375
- 0.9327
- 0.245
- 0.591
- 0,5039
- 0,4348
- 0,0764
- 0,318
- 18.124,89

- 0,2209
- 0,612
- 0,2255; 0,6128

- 0,9545

- 0.023
- 0

- 103
- 1684
- 64
Guía 9: Estadística Bayesiana
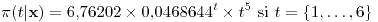
Media: 1,9356
Moda: 2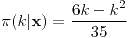 si
si 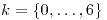
- 3
![<tex>\pi(\theta|5)=\frac{1}{2}(5-\theta)\mbox{ si }\theta\in[3,5]</tex> <tex>\pi(\theta|5)=\frac{1}{2}(5-\theta)\mbox{ si }\theta\in[3,5]</tex>](lib/plugins/latex/images/197281fdd823de013029c20dc7c595e93857a6d2_0.png)
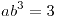
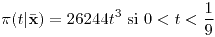
Media: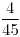
Moda: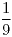
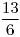
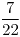

- Si hay 0 personas irritadas de las 10 encuestadas, la primera opinión (“poca gente irritada”) hará una buena estimación de
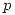 :
: 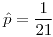 .
.
Si hay 0 personas irritadas de las 10 encuestadas, la segunda opinión (“mucha gente irritada”) hará una mala estimación de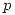 :
: 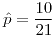 .
.
Si hay 10 personas irritadas de las 10 encuestadas, la primera opinión (“poca gente irritada”) hará una mala estimación de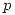 :
: 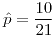 .
.
Si hay 10 personas irritadas de las 10 encuestadas, la segunda opinión (“mucha gente irritada”) hará una buena estimación de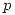 :
: 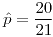 .
. 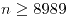
- Media:
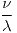
Moda: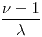

Media: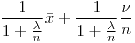
- Moda:
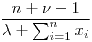
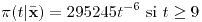
Media: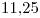
Moda: 9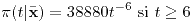
Media: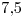
Moda: 6
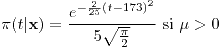
- Media: 173



Guía 10: Estimación Puntual
- Dado que
![<tex>ECM\left[\hat{\theta}_{1}\right]<ECM\left[\hat{\theta}_{2}\right]<ECM\left[\hat{\theta}_{3}\right]</tex> <tex>ECM\left[\hat{\theta}_{1}\right]<ECM\left[\hat{\theta}_{2}\right]<ECM\left[\hat{\theta}_{3}\right]</tex>](lib/plugins/latex/images/4d31d13c89cda6621ac2bb620de150c72eb52b8f_0.png) , el mejor estimador es
, el mejor estimador es 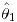 .
. 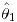 es insesgado.
es insesgado.
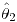 es sesgado.
es sesgado.
![<tex>ECM\left[\hat{p}_{2}\right]<ECM\left[\hat{p}_{1}\right]</tex> <tex>ECM\left[\hat{p}_{2}\right]<ECM\left[\hat{p}_{1}\right]</tex>](lib/plugins/latex/images/58dd7aea9459d2cdc02853aa6478605ef6b07f95_0.png) , el estimador
, el estimador 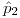 es preferible.
es preferible.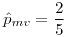
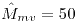
- -

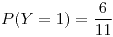


- No existe
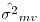
- El emv de la media es
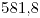
- El emv de la varianza es
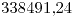
- El emv de la mediana es
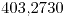
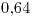


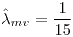
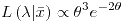
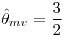
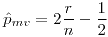
Guía 11: Estimación por Intervalos
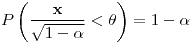
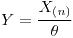 es un pivote para
es un pivote para 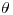 .
.![<tex> P\left(X_{(n)}<\theta<\frac{X_{(n)}}{\sqrt[n]{\alpha}}\right)=1-\alpha</tex> <tex> P\left(X_{(n)}<\theta<\frac{X_{(n)}}{\sqrt[n]{\alpha}}\right)=1-\alpha</tex>](lib/plugins/latex/images/95e0699b0aa9641252065eede1dce0cf5bd5f52e_0.png)
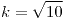
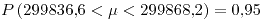
El intervalo de confianza dado sólo dice lo siguiente: “si realizas otra medición de la velocidad de la luz, hay un 95\% de probabilidad de que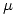 esté dentro de ese intervalo”.
esté dentro de ese intervalo”.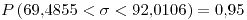

- 9604
![<tex>P\left[0.00021667<\lambda\right]=0.95</tex> <tex>P\left[0.00021667<\lambda\right]=0.95</tex>](lib/plugins/latex/images/9ed80d910dd38d34f7928be7d71a72a9774ada01_0.png)
- Proveedor 1.
Guía 12: Test de Hipótesis y Test de Bondad de Ajuste
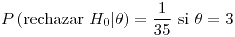
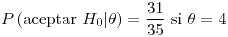
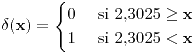
![<tex>P\left[\delta(\mathbf{x})=0|\mu=1.1\right]=0.876</tex> <tex>P\left[\delta(\mathbf{x})=0|\mu=1.1\right]=0.876</tex>](lib/plugins/latex/images/79c4efdd0499ebbdf123fcca9bf742fa23024d0d_0.png)
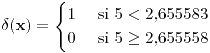
No rechazamos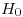 .
.- F
- V
- F
- F
- V
- F
- F
- V



![<tex>\delta(\mathbf{X})=\begin{cases} 1 & \text{ si }4\notin\left[\max\left\{ X_{i}\right\} ,1.3493\max\left\{ X_{i}\right\} \right]\\ 0 & \text{ si }4\in\left[\max\left\{ X_{i}\right\} ,1.3493\max\left\{ X_{i}\right\} \right]\end{cases}</tex> <tex>\delta(\mathbf{X})=\begin{cases} 1 & \text{ si }4\notin\left[\max\left\{ X_{i}\right\} ,1.3493\max\left\{ X_{i}\right\} \right]\\ 0 & \text{ si }4\in\left[\max\left\{ X_{i}\right\} ,1.3493\max\left\{ X_{i}\right\} \right]\end{cases}</tex>](lib/plugins/latex/images/713f77541f1c9b512e864cb64fe4ca3b3caaedeb_0.png)











- No se puede rechazar
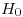 .
.
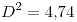
- No se puede rechazar
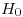 .
.
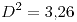
- No se puede rechazar
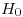 .
.

- No se puede rechazar
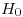 .
.
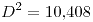
- No se puede rechazar
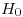 .
.


Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

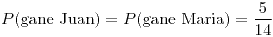
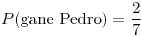
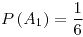

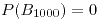






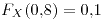
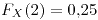
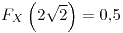
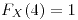
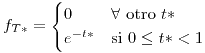
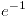
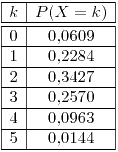
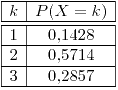
![<tex>\theta\in\left[-\frac{1}{2},\frac{1}{2}\right]</tex> <tex>\theta\in\left[-\frac{1}{2},\frac{1}{2}\right]</tex>](lib/plugins/latex/images/f9fafe8f0b73c3648d218e40b8090c2d3562c381_0.png)
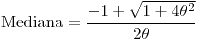
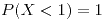
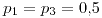

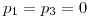

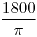
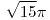
![<tex>E[S_{n}]=2n</tex> <tex>E[S_{n}]=2n</tex>](lib/plugins/latex/images/4ea6b47c73cb0184329b92ab3bf1daae05057bc8_0.png)
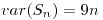
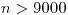
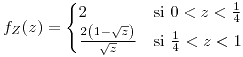
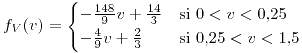
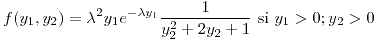
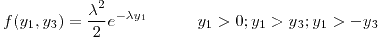
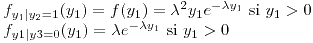
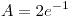
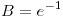
![<tex>E[Y|X]=X^{2}</tex> <tex>E[Y|X]=X^{2}</tex>](lib/plugins/latex/images/e1a7541554acbe86bb60a82621a7582fc195cc02_0.png)
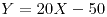
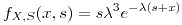
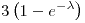
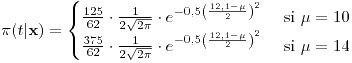
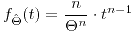
![<tex>B\left[\hat{\Theta}\right]=\Theta\left(\frac{n}{n+1}-1\right)</tex> <tex>B\left[\hat{\Theta}\right]=\Theta\left(\frac{n}{n+1}-1\right)</tex>](lib/plugins/latex/images/c9b546bbc5dbcd470b0ee148d2657df2dcccc5fe_0.png)
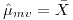
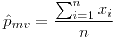
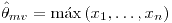
![<tex>\hat{\mu}_{mv}=\frac{1}{n}\left[\sum_{i=1}^{n}x_{i}\right]</tex> <tex>\hat{\mu}_{mv}=\frac{1}{n}\left[\sum_{i=1}^{n}x_{i}\right]</tex>](lib/plugins/latex/images/3586cd7d8152ef573f4fda44da32dca2301754f8_0.png)
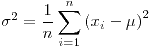
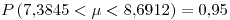
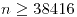
![<tex>X_{n+1}-\bar{X}_{n}\sim\mathcal{N}\left(0,\sigma^{2}\left[1-\frac{1}{n}\right]\right)</tex> <tex>X_{n+1}-\bar{X}_{n}\sim\mathcal{N}\left(0,\sigma^{2}\left[1-\frac{1}{n}\right]\right)</tex>](lib/plugins/latex/images/5b1d5557d91e76145f5e1dca715d9c64d9bfc322_0.png)
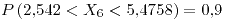
![<tex>P\left[0.07142<p<0.12878\right]\approx0.9</tex> <tex>P\left[0.07142<p<0.12878\right]\approx0.9</tex>](lib/plugins/latex/images/b2ea9ec21a74e773ad7258e7a92b1186e3dcde9f_0.png)
![<tex>P\left[0.0778<p\right]\approx0.9</tex> <tex>P\left[0.0778<p\right]\approx0.9</tex>](lib/plugins/latex/images/0b2570a2610a2860bf2c7eacffc8b9a72e3eee92_0.png)
![<tex>P\left[2.71275<\lambda<7.8525\right]=0.9</tex> <tex>P\left[2.71275<\lambda<7.8525\right]=0.9</tex>](lib/plugins/latex/images/1dafbe303d5c33f8864e8ef82e1aca8041bf96b9_0.png)
![<tex>P\left[2.78<5.4004\right]=0.9</tex> <tex>P\left[2.78<5.4004\right]=0.9</tex>](lib/plugins/latex/images/5fd5a47d6ae22c382f5c790f4f3d247921ee9dbb_0.png)
![<tex>P\left[0.15555<\lambda<1.02861\right]=0.95</tex> <tex>P\left[0.15555<\lambda<1.02861\right]=0.95</tex>](lib/plugins/latex/images/dedd73b57d278610c0debc2d21c1d96ab6d4e02f_0.png)
![<tex>P\left[0.4321<\Delta<56.31\right]=0.99</tex> <tex>P\left[0.4321<\Delta<56.31\right]=0.99</tex>](lib/plugins/latex/images/5e9eac17dd4bb0a2e009400997e3a55ca3380390_0.png)
![<tex>P\left[6.84<\Delta<49.9\right]=0.99</tex> <tex>P\left[6.84<\Delta<49.9\right]=0.99</tex>](lib/plugins/latex/images/effd058e203c121d70a43d0a9152a2b25a47904a_0.png)
![<tex>P\left[26.613<\Delta<30.128\right]=0.99</tex> <tex>P\left[26.613<\Delta<30.128\right]=0.99</tex>](lib/plugins/latex/images/577187210945394d7495ce5df5694839fcd0b156_0.png)
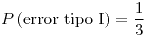
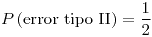
![<tex>pot(\theta)=\begin{cases}\left(\frac{2.9}{\theta}\right)^{n} & \text{ si }\theta\in[3,4]\\1 & \text{ si }\theta\in(0;2.9)\\\left(\frac{2.9}{\theta}\right)^{n} & \mbox{ si }\theta\in(2.9,3)\\\left(\frac{2.9}{\theta}\right)^{n}+1-\left(\frac{4}{\theta}\right)^{n} & \text{ si }\theta\in(4,\infty)\end{cases}</tex> <tex>pot(\theta)=\begin{cases}\left(\frac{2.9}{\theta}\right)^{n} & \text{ si }\theta\in[3,4]\\1 & \text{ si }\theta\in(0;2.9)\\\left(\frac{2.9}{\theta}\right)^{n} & \mbox{ si }\theta\in(2.9,3)\\\left(\frac{2.9}{\theta}\right)^{n}+1-\left(\frac{4}{\theta}\right)^{n} & \text{ si }\theta\in(4,\infty)\end{cases}</tex>](lib/plugins/latex/images/cfb534397bfe1075edbe935bb6e5ccae508efee5_0.png)
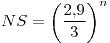
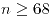
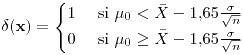
![<tex>\beta(\mu)=1-\phi_{\bar{X}_{(\mu,\sigma)}}\left[\mu_{0}+1.65\frac{\sigma}{\sqrt{n}}\right]</tex> <tex>\beta(\mu)=1-\phi_{\bar{X}_{(\mu,\sigma)}}\left[\mu_{0}+1.65\frac{\sigma}{\sqrt{n}}\right]</tex>](lib/plugins/latex/images/184cf1efb721f4b721664ffbf26e82227566b4e8_0.png)