Examen Parcial - 61.09. Probabilidad y Estadística B - 02/11/2013
Cátedra: Para todos
Fecha: 1 Oportunidad - 2º Cuatrimestre 2013
Día: 02/11/2013
Enunciado
Punto 1
Sea 
una variable aleatoria con función de distribución
.
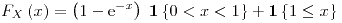Calcular ![<tex>E\left[X \middle| X>\ln\left(2\right)\right]</tex>](lib/plugins/latex/images/d6bb23f0e1fd87258e0bbcdaf63e62ef4a318a61_0.png "<tex>E\left[X \middle| X>\ln\left(2\right)\right]</tex>")
.
Punto 2
Lucas y Monk corren una carrera. Los tiempos (en minutos) que tardan en llegar a la meta son variables aleatorias exponenciales independientes, de media 10 para Lucas y de media 14 para Monk. Si el primero en llegar a la meta tardó 12 minutos, ¿cuál es la probabilidad de que haya sido Monk?
Punto 3
La distribución de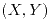 
es uniforme sobre el recinto sombreado que se muestra en la figura
Hallar la densidad conjunta de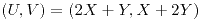 
y graficar la recta de regresión de 
basada en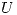 
.
Punto 4
Se realizará un experimento con un radioisótopo que emite partículas alpha de acuerdo con un proceso de Poisson de intensidad 3 por minuto. Para evitar intoxicaciones radiactivas se instala una alarma que suena cuando el tiempo entre dos emisiones consecutivas no supera 20 segundos. Calcular la esperanza del tiempo que transcurre desde que se inicia el experimento hasta que suena la alarma.
Punto 5
Se tienen dos monedas, una equilibrada y otra cargada con probabilidad 0.8 de cara. En cada tirada se elige una de las dos monedas y la probabilidad de elegir la moneda equilibrada es 0.25. Estimar la probabilidad de obtener más de 75 caras en 100 tiradas.
Resolución
