Examen Parcial - 61.09. Probabilidad y Estadística B

Cátedra: Grynberg
Fecha: 2° Recuperatorio - 2° Cuatrimestre 2011
Día: 07/12/2011

Se arrojan 7 bola en 7 urnas numeradas de 1 al 7. Las bolas son indistinguibles y todas las configuraciones distintas son equiprobables. Sabiendo que cayeron exactamente 3 bolas en la urna 2 calcular la probabilidad de que 2 bolas hayan caido en la urna 5 y las otras 2 en la urna 6.

Una máquina será utilizada en un proceso de producción durante 1 año. Las máquinas tienen un defecto de fabricación que hace que fallen una vez. Cuando la máquina falla se la repara inmediatamente y sigue funcionando sin fallas hasta que se cumple el plazo estipulado. El tiempo T (en años) hasta que ocurre la falla tiene distribución exponencial de media un año. Usando los números alearorios 0.46 y 0.72 simular dos valores del tiempo de uso de la máquina después de la reparación (0 si no hubo reparación).

Sean e 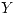dos variables aleatorias tales que y Hallar la expresión de la recta de regresión de 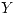dada .

Cierto alambre tiene fallas distribuidas según un proceso de Poisson de intensidad dos por metro. Las fallas pueden ser del tipo I o II. La probabilidad de que una falla sea de tipo I es el doble de la que sea de tipo II. Si en los primeros 10 metros de alambre se hallaron exactamente 15 fallas de tipo I, hallar la probabilidad que haya exactamente 1 falla (de cualquier tipo) en el primero de esos 10 metros de alambre.

Lucas y Monk compiten durante 50 encuentros en lanzamiento de jabalina. En cada encuentro cada uno de ellos lanza 2 veces la jabalina y su registro en ese encuentro es el máximo de las dos distancias alcanzadas. La distancia alcanzada en cada lanzamiento es una variable aleatoria con distribución uniforme entre 0 y 10 metros. Las distancias alcanzadas en los diversos lanzamientos son independientes. ¿Cuál es la probabilidad de que el promedio de los registros de Monk en los 50 encuentros supere al respectivo promedio de Lucas en más de un metro?