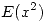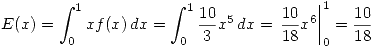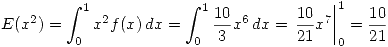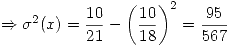Tabla de Contenidos
Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: 
Fecha: 
Día: 
Tema: 1
Enunciado
- Las variables
 e
e 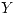 tienen la siguiente función densidad conjunta:
tienen la siguiente función densidad conjunta: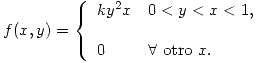
- Determinar la función densidad de
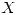 condicionada a
condicionada a 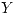 e indicar si las variables
e indicar si las variables 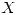 e
e 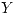 son independientes justificar la respuesta).
son independientes justificar la respuesta). - Determinar la curva regresión de
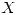 sobre
sobre 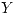 .
. - Hallar la media y varianza de
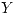 .
.
- Una fábrica recibe piezas producidas por tres subsidiarias,
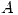 ,
, 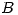 Y
Y 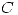 , las cuales producen el
, las cuales producen el 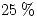 ,
, 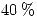 Y
Y 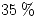 de las mismas, respectivamente. Se sabe que la producción de la subsidiaria
de las mismas, respectivamente. Se sabe que la producción de la subsidiaria 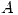 tiene un
tiene un 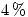 de defectuosos, la de la fábrica
de defectuosos, la de la fábrica 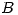 un
un 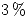 de defectuosos y la de la fábrica
de defectuosos y la de la fábrica 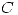 un
un 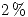 de defectuosos. Se pide:
de defectuosos. Se pide: - Hallar la probabilidad de que una pieza elegida al azar sea defectuosa.
- Calcular la probabilidad de que en un grupo de 6 piezas elegido al azar haya por lo menos una defectuosa.
- Si se extraen al azar en forma sucesiva 3 piezas hasta encontrar la primera pieza defectuosa, calcular la probabilidad de que dicha pieza provenga de
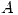 .
.
- Los clientes llegan a un lavadero de autos según un proceso de Poisson. De lunes a viernes el tiempo medio entre la llegada de dos clientes consecutivos es de 10 minutos. Se desea utilizar un programa de lavado automatizado que tiene un tiempo de respuesta
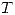 de 2 minutos (es decir, si llegan dos clientes separados por un intervalo menor que
de 2 minutos (es decir, si llegan dos clientes separados por un intervalo menor que 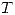 , el segundo no es atendido).
, el segundo no es atendido). - determinar la probabilidad
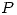 de que un cliente no sea atendido.
de que un cliente no sea atendido. - Indicar cuanto debe valer
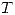 para que
para que 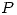 sea menor que 0.05.
sea menor que 0.05. - Si durante los fines de semana el tiempo medio entre la llegada de dos clientes consecutivos es de 30 minutos, calcular la probabilidad de que un cliente no sea atendido, si el tiempo de respuesta
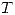 es el calculado en el item (b).
es el calculado en el item (b).
- El consumo diario de combustible de cada taxi de una ciudad puede modelizarse como una V.A. Normal con media 35 litros y desvío 2 litros. Si en una flota hay 100 taxis cuyo comportamiento es estadísticamente independiente, se pide:
- Calcular la capacidad del depósito para abastecer la flota durante 2 días de modo tal que la probabilidad de falta de combustible sea menor a 0.05.
- Si el depósito fue diseñado de acuerdo al valor calculado en (a), hallar la probabilidad de que en un día cualquiera se consuma menos del
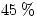 de su capacidad.
de su capacidad.
- Un buque para el transporte de naftas tiene 4 depósitos. La probabilidad de que un viaje cualquiera un depósito no se utilice (esté vacío) es
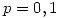 . Por otra parte, el contenido de cada depósito en uso es una V.A. Normal de media 70.000 litros y desvío 5.000 litros. Se pide:
. Por otra parte, el contenido de cada depósito en uso es una V.A. Normal de media 70.000 litros y desvío 5.000 litros. Se pide: - Hallar la probabilidad de que el volumen total transportado no supere los 135.000 litros si hay 2 depósitos vacíos.
- Si el precio de la nafta es
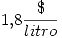 , calcular la probabilidad de que el valor de la carga supere 360.000
, calcular la probabilidad de que el valor de la carga supere 360.000 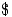 si hay 3 depósitos en uso.
si hay 3 depósitos en uso. - ¿ Cuál es la probabilidad de que haya 3 depósitos en uso?
Resolución
Punto I
Punto II
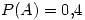 Probabilidad de que las piezas provengan de
Probabilidad de que las piezas provengan de 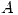 .
.
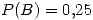 Probabilidad de que las piezas provengan de
Probabilidad de que las piezas provengan de 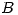 .
.
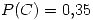 Probabilidad de que las piezas provengan de
Probabilidad de que las piezas provengan de 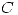 .
.
Se sabe que:
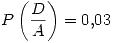 ,
, 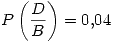 y
y 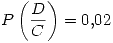
I

El 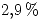 de las piezas son defectuosas.
de las piezas son defectuosas.
II
Para la resolución de este inciso se plantea una distribución binomial con 6 ensayos, donde la probabilidad de éxito es 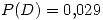 .
Entonces:
.
Entonces:
Sea 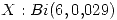 se pide
se pide 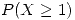
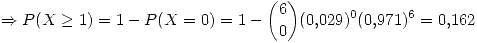
III
Cuando se trata de cantidad de ensayos realizados hasta conseguir el primer éxito se puede decir que está involucrada una distribución geométrica. En este caso se define 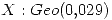 .
.
Lo que se pide en este inciso es 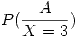
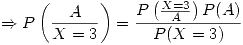
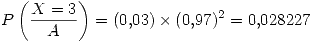
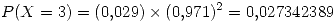
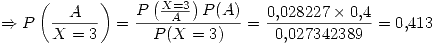
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported

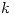 sabiendo que
sabiendo que 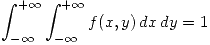
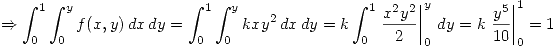
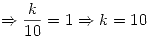
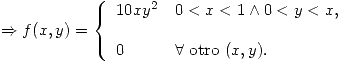


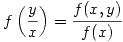
 :
:
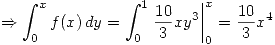
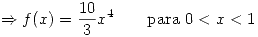
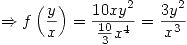
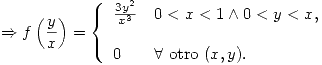
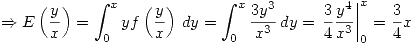
![<tex> \sigma^2(x) = E[x - E(x)]^2 = E\{x^2 - 2x\,E(x) + [E(x)]^2 \} = E(x^2) - [E(x)]^2</tex> <tex> \sigma^2(x) = E[x - E(x)]^2 = E\{x^2 - 2x\,E(x) + [E(x)]^2 \} = E(x^2) - [E(x)]^2</tex>](lib/plugins/latex/images/d285e03408863b1c93d3355509f6bac9c49b2f83_0.png)
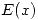 y
y