Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Grynberg
Fecha: 1° Recuperatorio - 2° Cuatrimestre 2008
Día: 12/11/2008
Enunciado
Punto I
Lucas pasea por el zoológico de Londres. 2/3 de los visitantes del zoológico son turistas y 1/3 son londinenses. Cuando se les pregunta por una dirección los turistas dan respuestas correctas con probabilidad 4/5 (Las respuestas a perguntas repetidas son independientes, inclusive si la pregunta y la persona son las mismas). Los londinenses siempre dan respuestas falsas. Lucas le pregunta a un visitante si los rinocerontes estan para el Este o para el Oeste. La respuesta es: “Para el Este”. Le pregunta de nuevo a la misma persona y recibe la misma respuesta. ¿Cual es la probabilidad de que la respuesta sea correcta?
Punto II
Sea U una variable aleatoria con distribución uniforme sobre el intervalo 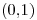 . Sea
. Sea  la longitud del intervalo
la longitud del intervalo  o
o 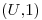 que contiene al punto
que contiene al punto 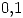 . Hallar la funcion de distribución de
. Hallar la funcion de distribución de 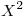
Punto III
Sea  un punto aleatorio con distribución uniforme en el triangulo de vértices
un punto aleatorio con distribución uniforme en el triangulo de vértices 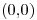 ,
,  ,
,  . Usando el número aleatorio
. Usando el número aleatorio  simular un valor de la variable aleatoria
simular un valor de la variable aleatoria  .
.
Punto IV
Una gallina pone huevos de acuerdo con proceso de Poisson de intensidad 12 por dia. De cada huevo nace un pollo con probabilidad 5/6 independientemente de los demas. Calcular la covarianza entre la cantidad de huevos que pone la gallina durante una semana y la cantidad de pollos nacidos esa semana.
Punto V
972 números se redondean al entero más cercano y se suman. Si los errores individuales de redondeo se distribuyen uniformemente sobre el intervalo (-0.5,0.5), aproxima la probabilidad de que la suma resultante difiera de la suma exacta en más de 9.
Resolución
Punto I
Defino:



Realizando un diagrama del arbol, nos queda:
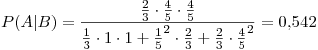
Punto II
Punto III


Calculo la densidad como ancho sobre area:
 Si
Si ![<tex>x \in [0.5]</tex> <tex>x \in [0.5]</tex>](lib/plugins/latex/images/a1c2faefa70347e291cfb3c490a5c184f8bc10d4_0.png)
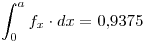
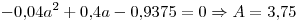
Punto IV
Defino:
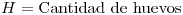
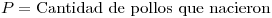
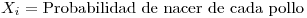
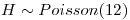
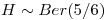
![<tex>E[H] = 12 \cdot 7 = 84</tex> <tex>E[H] = 12 \cdot 7 = 84</tex>](lib/plugins/latex/images/09ab0938851001b83ff01a59a2c2396802f42772_0.png)

![<tex>E[x_i] = 5/6</tex> <tex>E[x_i] = 5/6</tex>](lib/plugins/latex/images/c110f1970d064c30afba3d820f894fdc126d0503_0.png)
![<tex>E[P] = 70</tex> <tex>E[P] = 70</tex>](lib/plugins/latex/images/4062ca3c4a2067d607d3c48d247fbf898999cb92_0.png)
![<tex>E[H \cdot P] = E[E[P \cdot H | H ] = E[H \cdot E[P|H] = \frac{5}{6} \cdot E[H^2]</tex> <tex>E[H \cdot P] = E[E[P \cdot H | H ] = E[H \cdot E[P|H] = \frac{5}{6} \cdot E[H^2]</tex>](lib/plugins/latex/images/45d136c2f0c7a2e5169a5b8cf3dc9bbcaa0830d8_0.png)
![<tex>V[H] = E[H^2] - E[H]^2 \Rightarrow E[H^2] = 7140 \Rightarrow E[H \cdot P] = 5960</tex> <tex>V[H] = E[H^2] - E[H]^2 \Rightarrow E[H^2] = 7140 \Rightarrow E[H \cdot P] = 5960</tex>](lib/plugins/latex/images/54737101fe825e585629d185839d093bfeebe0cb_0.png)
![<tex>Cov(H,P) = E[H \cdot P] - E[H] \cdot E[P] = 70 </tex> <tex>Cov(H,P) = E[H \cdot P] - E[H] \cdot E[P] = 70 </tex>](lib/plugins/latex/images/8ce5f5663677841023778574b1f04902e817540c_0.png)
Punto V
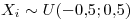
![<tex> E[xi] = 0</tex> <tex> E[xi] = 0</tex>](lib/plugins/latex/images/7a5ec2fd570552f7d229d7fca61aa470522f84a4_0.png)
![<tex> V[xi] = \frac{1}{12}</tex> <tex> V[xi] = \frac{1}{12}</tex>](lib/plugins/latex/images/051b5ca155ead109824c6b2d5f7fb7165ac4f578_0.png)

Hay que calcular via teorema central del limite: