Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Rey
Fecha: 1° Recuperatorio - 1° Cuatrimestre 2008
Día: 06/06/2008
Enunciado
Punto I
Para el estreno de la película “Los 4 fantásticos XXIV” , la empresa que fabrica los famosos huevitos con “sorpresa” decide lanzar una colección de muñequitos con los 4 personajes. Suponga que cada vez que se compra un huevo, todos los personajes tienen igual probabilidad de aparecer y la aparición de los personajes en cada huevo se produce en forma independiente. Sea N la “cantidad de huevos que hay que comprar hasta completar la colección” (al menos uno de cada uno). Hallar la media y varianza de N.
Punto II
Se tienen 2 urnas . Cada una contiene 2 monedas falsas; en la urna 1 las monedas tienen probabilidad de cara p1 y en la 2, p2≠p1.Puede optar por una de dos estrategias:
- (a)Elegir una urna al azar y tirar ambas monedas.
- (b)Elegir una moneda de cada urna y lanzarlas.
Si se gana el juego cuando ambas monedas salen cara, defina cúal de las dos estrategias es más conveniente.
Punto III
Se tiene una barra de N metros de largo (N es un numero fijo). Se eligen dos puntos de corte al azar y en forma independiente. Al cortar, resultan 3 pedazos. Halle la probabilidad de poder formar un triángulo con dichos pedazos.
Punto IV
X e Y son U(0,1) e independientes. Sean Q = Y - X y R = Y + X. Hallar la covarianza entre Q y R.
¿Qué puede decir sobre la independencia entre Q y R?
Punto V
Sean X|K VAs exponenciales de parámetro λ=K, donde K es una VA que toma los valores 1 ó 2 con igual probabilidad.
- (a)Calcule P(K=1|X=2)
- (b)Halle E(e-5X)
- (c)Sea L=K3. De todas las funciones g(L), encuentre una expresión explícita para la que minimiza E[(X-g(L))2]
- (d)Halle la probabilidad de que el promedio de 50 valores de X i.i.d. sea mayor a 1
Resolución
Punto I
Podemos definir a N como:

Donde:
 :cantidad de extracciones desde la primera hasta obtener el 2° muñeco
:cantidad de extracciones desde la primera hasta obtener el 2° muñeco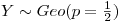 :cantidad de extracciones desde la
:cantidad de extracciones desde la  esima hasta obtener el 3° muñeco
esima hasta obtener el 3° muñeco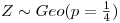 :cantidad de extracciones desde la
:cantidad de extracciones desde la  esima hasta obtener el 4° muñeco
esima hasta obtener el 4° muñeco
Entonces por propiedades de la esperanza:
![<tex>E[N]=1+E[X]+E[Y]+E[Z]</tex> <tex>E[N]=1+E[X]+E[Y]+E[Z]</tex>](lib/plugins/latex/images/57b00b8addc5a3b4214ba691e9424e12c550ffdc_0.png)
Como X,Y,Z poseen distribución Geo:  y
y 
Reemplazando:
![<tex>E[N]=1+\frac1{\frac34}+\frac1{\frac12}+\frac1{\frac14}=\frac{25}3=8.33</tex> <tex>E[N]=1+\frac1{\frac34}+\frac1{\frac12}+\frac1{\frac14}=\frac{25}3=8.33</tex>](lib/plugins/latex/images/9aa4791da77df0e52a258b365785775707a05899_0.png)
Si asumimos que las tres variables son independientes, es decir no importa cuantos tiros hayamos hecho para sacar el próximo muñeco, entonces tendremos por propiedades de la varianza:

Punto II
La estrategia más conveniente será aquella que tenga mayor probabilidad. Para ello definimos los siguentes eventos:
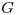 :Evento ganar
:Evento ganar
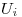 :Evento elegir urna i
:Evento elegir urna i
 :Evento sacar cara en la moneda iesima
:Evento sacar cara en la moneda iesima
Para la estrategia (a) tendremos por probabilidad total que la probabilidad de ganar será:



Analogamente para la estrategia (b) la probabilidad de ganar será

Operando con 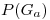
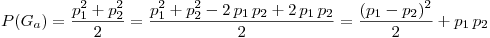
Es obvio que 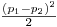 es mayor a 0 por ende la estrategia (a) es la más conveniente
es mayor a 0 por ende la estrategia (a) es la más conveniente
Punto III
Para que se forme un triangulo, la longitud de la suma de dos lados tiene que ser mayor a la longitud del tercer lado.
Las ecuaciones nos quedan:



Se puede calcular graficamente y el resultado da: 
