Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primer Recuperatorio - Primer Cuatrimestre 2008
Día: 27/05/2008
Tema: 2
Enunciado
- Para completar un trabajo deben realizarse las operaciones
 ,
,  y
y  (en forma consecutiva). Los tiempos en días que tarda cada operación son VAN independientes de parámetros
(en forma consecutiva). Los tiempos en días que tarda cada operación son VAN independientes de parámetros  ;
; 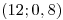 y
y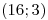 . (a) Encontrar la probabilidad de que el tiempo total para completar el trabajo sea mayor de 42 días teniendo en cuenta que el tiempo que se demora para pasar de una operación a la siguiente es fijo de 1,5 días. (b) Calcular la probabilidad de que el tiempo desde el inicio de la operación A hasta el inicio de la operación C sea menor que el tiempo necesario para la ejecución de la operación C.
. (a) Encontrar la probabilidad de que el tiempo total para completar el trabajo sea mayor de 42 días teniendo en cuenta que el tiempo que se demora para pasar de una operación a la siguiente es fijo de 1,5 días. (b) Calcular la probabilidad de que el tiempo desde el inicio de la operación A hasta el inicio de la operación C sea menor que el tiempo necesario para la ejecución de la operación C. - La cantidad de vehículos que pasan por un control policial por minuto tiene una dist. Poisson de media 10. Cada 2 minutos se controlan 4 vehículos. Se sabe que en promedio el 10% de los vehículos no están en condiciones de circular. Cuando un vehículo que es controlado no aprueba el control queda demorado. (a) Calcular la probabilidad de que en los próximos 4 minutos quede demorado por lo menos un vehículo. (b) ¿Cual es la probabilidad de que en el próximo minuto no pase ningún vehículo?
- Se enfrentan en un partido de fútbol dos equipos con respectivas tasas de goles a favor por partido igual a dos. ¿Qué es más probable, que el partido termine empatado o no empatado?
- Sea
 , donde las
, donde las 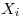 tienen fdp
tienen fdp  . Obtener
. Obtener 
Resolución
Punto I
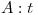 en días
en días 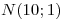
 en días
en días 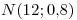
 en días
en días 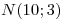
(a)


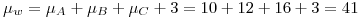
![<tex>\sigma_w = \sqrt[2]{\sigma_A^2+\sigma_B^2+\sigma_C^2}=\sqrt[2]{1^2+(0.8)^2+3^2}=3.2619</tex> <tex>\sigma_w = \sqrt[2]{\sigma_A^2+\sigma_B^2+\sigma_C^2}=\sqrt[2]{1^2+(0.8)^2+3^2}=3.2619</tex>](lib/plugins/latex/images/55cbefcf0e90f2f55b1cdda91a47cad66c8fe635_0.png)
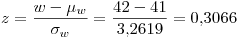

(b)

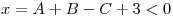
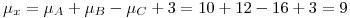
![<tex>\sigma_x = \sqrt[2]{\sigma_A^2+\sigma_B^2+{-1}^2\sigma_C^2}=\sqrt[2]{1^2+(0.8)^2+3^2}=3.2619</tex> <tex>\sigma_x = \sqrt[2]{\sigma_A^2+\sigma_B^2+{-1}^2\sigma_C^2}=\sqrt[2]{1^2+(0.8)^2+3^2}=3.2619</tex>](lib/plugins/latex/images/7a7cee2947e6f0c84ee73fb500a9cbc331210328_0.png)

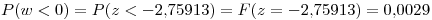
Punto II
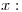 Cantidad de vehículos que pasan por un control por minuto
Cantidad de vehículos que pasan por un control por minuto
Como la media es 

(a)
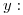 Cantidad de vehículos demorados en 4 minutos
Cantidad de vehículos demorados en 4 minutos

 está dado por una dist. Binomial
está dado por una dist. Binomial  , donde
, donde 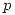 es la probabilidad de éxito es decir la probabilidad de que un vehículo no esté en condiciones o sea
es la probabilidad de éxito es decir la probabilidad de que un vehículo no esté en condiciones o sea  . Y
. Y  es la cantidad de ensayos, en este caso sería la cantidad de vehículos controlados o sea
es la cantidad de ensayos, en este caso sería la cantidad de vehículos controlados o sea  (porque se controlan 4 cada 2 minutos y se están tomando 4 minutos).
(porque se controlan 4 cada 2 minutos y se están tomando 4 minutos).


(b)
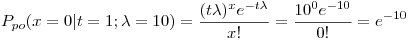
Punto III
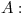 goles del primer equipo
goles del primer equipo
 goles del segundo equipo
goles del segundo equipo
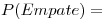
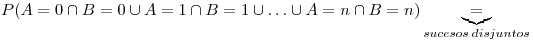
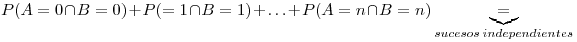

![<tex>P(A=0)^2+P(=1)^2+\ldots +P(A=n)^2=\sum_{i=0}^n{[P(A=i)]^2}</tex> <tex>P(A=0)^2+P(=1)^2+\ldots +P(A=n)^2=\sum_{i=0}^n{[P(A=i)]^2}</tex>](lib/plugins/latex/images/606b538e5a600d324099e88340be3b44410a2735_0.png)

![<tex>P(Empate)=\sum_{i=0}^n{[P(A=i)]^2}=\sum_{i=0}^n{[\frac{3^i e^{-3}}{i!}]^2}\approx 0.167</tex> <tex>P(Empate)=\sum_{i=0}^n{[P(A=i)]^2}=\sum_{i=0}^n{[\frac{3^i e^{-3}}{i!}]^2}\approx 0.167</tex>](lib/plugins/latex/images/1aa769632fe94756d80cb7a6c3aa7fcd35301dda_0.png)
 Es más probable que el partido no termine empatado
Es más probable que el partido no termine empatado
Punto IV


Como los  valores
valores 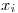 son independientes (porque no se aclara lo contrario) e identicamente distribuidos, se puede usar esta formula :
son independientes (porque no se aclara lo contrario) e identicamente distribuidos, se puede usar esta formula :
![<tex>F(X_{max}=x)=[F(X=x)]^n</tex> <tex>F(X_{max}=x)=[F(X=x)]^n</tex>](lib/plugins/latex/images/c769153faf88bc99b9d7efe07e0032420b26b3d6_0.png)
![<tex>f(X_{max}=x)=n[F(x=X)]^{n-1}f(X=x)=n\frac{x^{n-1}}{b^n}</tex> <tex>f(X_{max}=x)=n[F(x=X)]^{n-1}f(X=x)=n\frac{x^{n-1}}{b^n}</tex>](lib/plugins/latex/images/87353cca484ea6b097f3a2ef639c28df91bb963d_0.png)

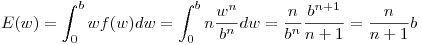
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
