Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primer Recuperatorio - Segundo Cuatrimestre 2007
Día: 21/11/2007
Tema: 2
Enunciado
- El peso (en kg) de ciertos artículos es una variable aleatoria
 cuya función de densidad de probabilidad es:
cuya función de densidad de probabilidad es:  si
si 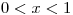 ;
; 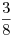 si
si 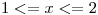 ;
;  si
si 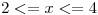 ; nula
; nula  otro
otro  . Se descartan aquellas cuyo peso sea inferior a 1 kg. Los artículos restantes se venden al público. El precio de venta depende del peso del mismo y está dado por
. Se descartan aquellas cuyo peso sea inferior a 1 kg. Los artículos restantes se venden al público. El precio de venta depende del peso del mismo y está dado por  . Determinar el precio medio de venta de cada artículo y la probabilidad de que al elegir un artículo al azar, resulte tener un precio de venta superior a $27.
. Determinar el precio medio de venta de cada artículo y la probabilidad de que al elegir un artículo al azar, resulte tener un precio de venta superior a $27. - En un proceso de fabricación de tornillos, intervienen 2 máquinas. La máquina A genera el 60% de la producción y trabaja con un 6% de piezas defectuosas, mientras que la máquina B se encarga del resto de la producción pero trabajando con un 9% de piezas defectuosas. En un día determinado, se extraen dos tornillos al azar y resultan ser defectuosos; determine la probabilidad de que ambos hayan sido fabricados por la máquina B.
- La venta diaria de nafta super en una estación de servicio tiene media 4000 litros y desvío de 800 litros. El depósito de nafta super de la estación tiene capacidad para 60000 litros y se recomienda que se lo mantenga al menos con 10000 litros. Si actualmente el depósito está lleno, ¿dentro de cuantos días deberá volver a llenarse para tener 95% de probabilidad de que el tanque no quede en ningún momento con menos de 10000 litros? Indique claramente todas las hipótesis necesarias para hacer el cálculo.
- El diámetro de ciertas esferas (en cm.) es una variable aleatoria
 y el peso de las mismas (en gr.) es otra variable aleatoria
y el peso de las mismas (en gr.) es otra variable aleatoria 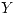 ambas constituyen una variable aleatoria cuya función de densidad conjunta es:
ambas constituyen una variable aleatoria cuya función de densidad conjunta es: 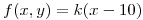 con
con  ;
;  ; nula para el resto. Determine si el peso y el diámetro son estadísticamente independientes y determine también si la función de regresión del diámetro dado el peso es una función lineal.
; nula para el resto. Determine si el peso y el diámetro son estadísticamente independientes y determine también si la función de regresión del diámetro dado el peso es una función lineal.
Resolución
Punto I
Punto II
Se definen ante todo las variables aleatorias a utilizar:
A = probabilidad que el artículo haya salido de A.
B = probabilidad que el artículo haya salido de B.
D = probabilidad que el artículo sea defectuoso.
Los datos en función de las v.a.:


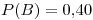

Aplicando probabilidad total obtenemos P(D):
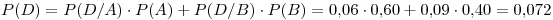
Se necesita la probabilidad de que un artículo haya salido de B sabiendo que es defectuoso. Usamos la regla de Bayes:
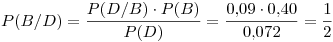
La probabilidad de obtener  tornillos defectuosos de B sacando de a
tornillos defectuosos de B sacando de a  tornillos es una distribución binomial con
tornillos es una distribución binomial con  y
y 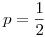 .
.

Ahora para obtener la probabilidad de que 2 tornillos hayan provenido de B evaluo la binomial en 

Nota: Para la distribución binomial supusimos que los dos sucesos son independientes, por lo tanto:

Punto III
La venta diaria está definida como una  .
.
Aplicando propiedades reproductivas de las normales, para  y
y  dadas y asumiendo independencia entre cada normal, las resultantes serán:
dadas y asumiendo independencia entre cada normal, las resultantes serán: 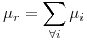 ,
, 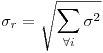 .
.
De ahí, y sabiendo que nuestra carga diaria son VA normales, independientes entre sí, y con  y
y 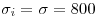 ; entonces obtenemos, que el consumo, para una
; entonces obtenemos, que el consumo, para una  cantidad de días estará será una
cantidad de días estará será una  .
.
El tanque tiene 60000 litros; pero como queremos tener 10000 litros de margen, nos interesa mirar el punto en el cual se sobrepasan los 50000 litros de consumo. Dada la normal que representa el consumo, nos interesará hallar el valor límite de  para la cual el 95% del peso de la función se encuentra antes de 50000; es decir, habrá al menos un 95% de probabilidades de que no se alcancen los 50000 litros de consumo, lo que nos dejará 10000 litros de margen para nuestro tanque de 60000 litros.
para la cual el 95% del peso de la función se encuentra antes de 50000; es decir, habrá al menos un 95% de probabilidades de que no se alcancen los 50000 litros de consumo, lo que nos dejará 10000 litros de margen para nuestro tanque de 60000 litros.
Para una  , el 95% con exceso se alcanza para
, el 95% con exceso se alcanza para  .
.
Siendo  nuestra variable en litros para el consumo; la relación entre esta variable y
nuestra variable en litros para el consumo; la relación entre esta variable y  estará dada por
estará dada por 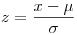 ; en donde, por lo calculado antes,
; en donde, por lo calculado antes,  y
y 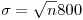 .
.
Juntando todo, la condición de no alcanzar los 50000 litros de consumo con un 95% de margen; se traduce en que para 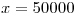 estamos en el límite para
estamos en el límite para  ; de ahí planteamos la inecuación:
; de ahí planteamos la inecuación:
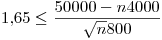
Buscamos el  mayor que satisfaga:
mayor que satisfaga:
- Para
 , el término de la derecha es
, el término de la derecha es  ; lo cual no valida.
; lo cual no valida. - Para
 , el término de la derecha da
, el término de la derecha da 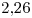 ; el cual es válido.
; el cual es válido.
Dado que ese  representa la cantidad de días y ese es un valor discreto, entonces el último satisface lo pedido.
representa la cantidad de días y ese es un valor discreto, entonces el último satisface lo pedido.
Actualizando nuestros valores de  para el valor encontrado y revisando en tablas; podemos afirmar que: Si el tanque se llena a los 11 días, se tiene el 98% de certeza de que no se alcanzarán los 50000 litros de consumo. En cambio, si esperáramos un día más, tendríamos apenas el 76% de certeza de ello.
para el valor encontrado y revisando en tablas; podemos afirmar que: Si el tanque se llena a los 11 días, se tiene el 98% de certeza de que no se alcanzarán los 50000 litros de consumo. En cambio, si esperáramos un día más, tendríamos apenas el 76% de certeza de ello.
