Examen Parcial - 61.09. Probabilidad y Estadística B

Cátedra: Baliña
Fecha: Primer Parcial - Segundo Cuatrimestre 2007
Día: 31/10/2007
Tema: 3

1. En una fábrica se producen dos tipos de artículos, “A” y “B”. La probabilidad de que “A” sea procesado correctamente es del 96% y para “B” vale 98%. Se recibe un pedido de 3 artículos del tipo “A” y 4 del tipo “B”. ¿ Cuál es la probabilidad de que en total deban procesarse más de 10 para cumplir el pedido?
2. La cantidad de cortes de servicio mensuales que se producen en un sistema informático tiene distribución Poisson de media 7. La duración de cada corte tiene función de densidad de probabilidad (fdp) 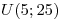en minutos. Si en el último mes se sabe que hubo 1 o 2 cortes, encontrar la fdp del tiempo total de corte de servicio.
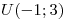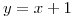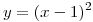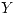3. Sea una variable aleatoria con fdp . Sea el cambio de variables si ; si . Encontrar la fdp de . Graficar.
4. Se tiene una urna con 3 bolillas blancas y 4 negras (urna 1) y otra con sólo 2 negras (urna 2). Se arroja un dado y si se obtiene 1, 2, 3 o 4 se pasa una bolilla de la urna 1 a la 2. En cambio, si se obtiene un 5 o un 6 en el dado, se pasan 2 bolillas ¿Cuál es la distribución de la cantidad de negras al final en la urna 2?

Se utiliza una distribución hipergeométrica con , , (si sale 1,2,3 o 4 en el dado) o (si sale 5 o 6 en el dado).

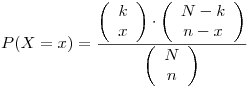
Además sabemos que:

P(1,2,3 o 4 en el dado) =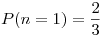

P(5 o 4 en el dado) =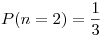

La distribución de la cantidad de negras en la urna 2 es:

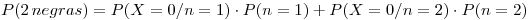
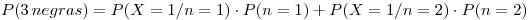
Calculamos los datos que nos faltan:

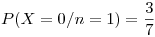
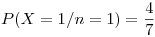
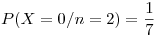
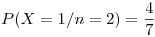
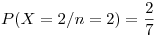
Reemplazamos los datos y obtenemos la distribución:

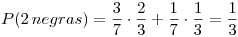
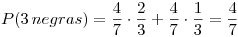
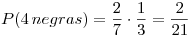
para todo otro valor

Se puede verificar que si sumamos los valores: .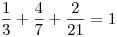

También se puede resolver por Bayes, pero el ejercicio tendría muchas más cuentas.