Examen Parcial - 61.09. Probabilidad y Estadística B

Cátedra: Rey
Fecha: 1° oportunidad - 1° Cuatrimestre 2007
Día: 19/05/2007

En un contenedor hay 6 naranjas y 4 limones. Estas frutas fueron adquiridas a un productor que especifica que el peso de las mismas (en gramos) sigue una distribución Normal(110, 10) para las naranjas y Normal(100, 11) para los limones. Se extraen del contenedor 2 frutas al azar sin resposición y se las coloca en una bolsa (de peso despreciable).

1. Calcular la probabilidad de que el peso de la bola llena sea mayor a 210 gramos.
2. Sabiendo que el peso de la bola llena es exactamente 200 gramos, hallar la probabilidad de que se hallan colocado 2 limones en la bolsa.

En una ruta, los vehículos atraviesan un puesto de peaje con una tasa de 10 por minuto. Los vehículos son autos en el 70% de los casos, motos en el 10% y camiones en un 20%.

1. Hallar la cantidad de media de autos que cruzan el peaje por minuto (Cuidado!).
2. Hallar la probabilidad de que en 1 minuto pasen 7 autos, 2 camiones y 1 moto.

Sean X e Y dos Variables Aleatorias independientes con medidas , , , .

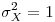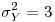1. Se elige un valor de X y otro Y, y se construyen las variables 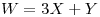y . Hallar la covarianza entre W y Z. ¿Son W y Z independientes?
2. Se toman ahora 100 valores independientes de X e Y. De acuerdo con la definición previa de las variables W y Z, justifique cuidadosamente qué distribución aproximada tendrá la variable:

A comienzos de diciembre del 2001, los depósitos en caja de ahorro de un cierto banco estaban distribuidas exponencialmente con media $3000. Un simpático decreto determinó que no se podría retirar en un mes más de $1000. Ante esto, durante dicho mes la gente se decontroló e intento extraer todo el dinero posible de sus cuentas. Sin embargo, otros no pudieron (o quisieron) soportar las enormes colas necesarias par ello. Al terminar el mes, el 75% de los clientes del banco logró extraer todo lo posible (el resto de los clientes “mantuvo sus depósitos sin movimientos”). Si no se consideran los ingresos que tuvieron las cuentas de dcicho banco durante ese mes,

1. Hallar la distribución de los depósitos del banco al finalizar el mes de diciembre.
2. Calular la cantidad media de dinero en los depósitos al finalizar diciembre.

Se elige un número al azar comprendido entre -2 y 2. Luego se elige otro (independiente del primero) comprendido entre 3 y 5. Encuentre la función densidad de la diferencia entre el cuadrado del primero y el segundo.