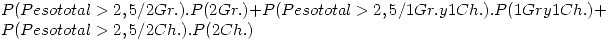Enunciado
Punto I
El tiempo de vida de un componente eléctrico es una variable aleatoria exponencial negativa de media 3 años.
- Se puso a prueba tres componentes elegidos al azar de la producción.¿Cuál es la prob. de que dos de ellos hayan durado más de 3 años? ¿Cuál es la prob. de que el que falló primero de los 3 probados, halla durado más de 3 años?
- El fabricante de estos componentes ofrece una garantía de 1 año. El precio de venta de cada componente es $200. Si un componente entra en reparaciòn durante el período de garantía, el costo para repararlo es $50. ¿Cuál es la función de densidad de prob. de la ganancia que obtiene el fabricante al vender un componente? ¿Cuál es la ganancia media?.
Punto II
En una caja de 10 piezas, hay 4 piezas grandes y 6 chicas. Las grandes tienen un peso que es una variable aleatoria normal de media 3 kg. y desvío estándar 0,75 kg. Las chicas tienen un peso que se distribuye según una ley normal de media 2 2 kg. y desvío 0,5 kg. Se extraen 2 piezas de la caja sin reposición. Si el peso total en la muestra extraída es mayor a 2,5 kg., ¿Cuál ees la probabilidad de que se hayan extraído una grande y una chica?.
Punto III
El peso (en gr.) de sardinas grandes es una variable aleatoria cuya función de densidad de prob. es:
 .
.
El peso de sardinas chicas es una variable aleatoria uniforme U[20;50]. Las latas de 10 sardinas se llenan con 4 sardinas grandes y 6 chicas. A) ¿Cuál debe ser el peso nominal neto a indicar en las latas para que el 3% de las latas contenga menos de lo indicado? B) ¿Cuál es probabilidad de que haya en cada lata mas peso de sardinas chicas que de grandes? Indique la aproximación necesaria para resolver el problema. Justificando dicha aproximación.
Punto IV
El volumen (litros) que ocupa un gas depende de su temperatura y presión a la que esté sometida. La presión P (en ATM) la temperatura T (º K Kelvin) son variables aleatorias cuya función de densidad de probabilidad conjunta es:
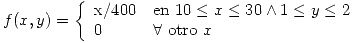 .
.
La ley de los gases ideales es: N.R.T. = P.V , siendo R una constante universal para todos los gases ideales igual a 0,082 (ATM L/K.mol) y N: numero de moles de atomos de gas.
- ¿Cuál es la probabilidad de que el volumen que ocupan 24,4 moles de un gas supere los 20 litros?
- ¿Halle la función de densidad de probabilidad de volumen que ocupan 24,4 moles de un gas?
- ¿La presion P y la temperatura T, son variables aleatorias independientes? Justifique su respuesta aplicando la definición de independencia.
- ¿Cuál es la función de regresión de la presion dada una temperatura?
Solución
Punto II
 Extrae 1 Grande y 1 Chica
Extrae 1 Grande y 1 Chica Peso total
Peso total 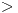 2.5
2.5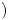 =
= 
 =
=