Tabla de Contenidos
Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primer Recuperatorio - Segundo Cuatrimestre 2006
Día: 15/11/2006
Tema: 1
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- Sea
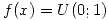 . Sea
. Sea 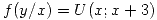 . Hallar la media de ”
. Hallar la media de ”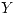 ”.
”. - Una máquina corta un rollo de tela cuando detecta una falla. La probabilidad de detectar cada falla vale
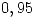 . Si la tasa de fallas por unidad de longitud del rollo de tela vale
. Si la tasa de fallas por unidad de longitud del rollo de tela vale 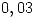 ; encontrar la función de probabilidad de la cantidad de fallas por rollo.
; encontrar la función de probabilidad de la cantidad de fallas por rollo. - Determinado tipo de vehículo puede transportar hasta
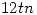 de carga. Si se van a transportar cajas con peso de media
de carga. Si se van a transportar cajas con peso de media 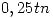 y desvío de
y desvío de 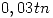 , cuántas cajas deberán colocarse por vehículo si se desea una probabilidad menor del 1% de superar la capacidad de carga del camión?
, cuántas cajas deberán colocarse por vehículo si se desea una probabilidad menor del 1% de superar la capacidad de carga del camión? - Dada
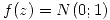 y sabiendo que
y sabiendo que  ; encontrar el resultado numérico de
; encontrar el resultado numérico de 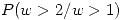 .
.
Resolución
Punto I
Por definición 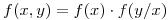
Sean
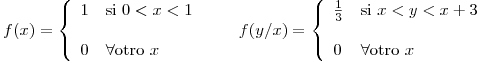
Se obtiene
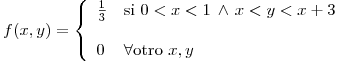
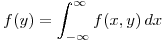
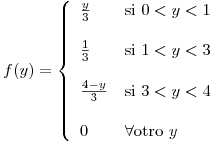
![<tex>E[y] = \int_{-\infty}^\infty y f(y) \,dy = 2</tex> <tex>E[y] = \int_{-\infty}^\infty y f(y) \,dy = 2</tex>](lib/plugins/latex/images/ca68262b870d25e5a5ea7edb995cec65684a7219_0.png)
Punto II
Punto III
Para resolver este problema se supone que la cantidad de cajas es mayor a 30. Esto permite resolver el problema mediante el teorema central del límite; luego si se comprueba la hipotesis la cantidad calculada de cajas será válida.
Se debe calcular 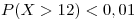 donde
donde 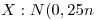 ;
;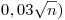 y
y  es la cantidad de cajas.
es la cantidad de cajas.
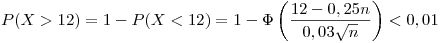
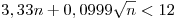

Punto IV
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
