Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primera Oportunidad - Segundo Cuatrimestre 2006
Día: 25/10/2006
Tema: 2
Enunciado
- Sea
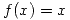 en
en 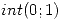 ;
; 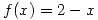 en
en 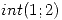 ; nula para el resto
; nula para el resto
Sea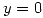 si
si 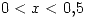 ;
; 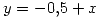 si
si 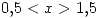 ;
; 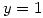 si
si 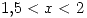
Encontrar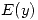 y
y 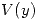
- La cantidad X de penales a favor por partido que se sancionan para determinado equipo tiene distribución
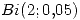 . El DT ha decidido mantener al mismo ejecutante de penales hasta que falle. En ese caso designa a un nuevo ejecutante, reemplazándolo cuando falle y así sucesivamente. La probabilidad de que un jugador (cualquiera) falle un penal vale
. El DT ha decidido mantener al mismo ejecutante de penales hasta que falle. En ese caso designa a un nuevo ejecutante, reemplazándolo cuando falle y así sucesivamente. La probabilidad de que un jugador (cualquiera) falle un penal vale 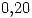 . Si el próximo torneo tiene 19 partidos cual es la probabilidad de que al finalizar el mismo, el DT haya cambiado al menos 1 vez al ejecutatne de penales?
. Si el próximo torneo tiene 19 partidos cual es la probabilidad de que al finalizar el mismo, el DT haya cambiado al menos 1 vez al ejecutatne de penales? - Sea
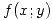 constante en el recinto limitado por los vertices de coordenadas
constante en el recinto limitado por los vertices de coordenadas 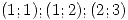
Encontrar la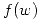 si
si 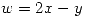
- La cantidad de personas que suben a un ascensor en PB teine distribución
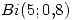 . El peso en Kg de cada persona tiene distribución Gamma con
. El peso en Kg de cada persona tiene distribución Gamma con 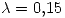 y
y  . Si se sabe que el ascensor salio de PB llevando un peso inferior a 200Kg, cual es la probabilidad de que hayan subido menos de 4 personas?
. Si se sabe que el ascensor salio de PB llevando un peso inferior a 200Kg, cual es la probabilidad de que hayan subido menos de 4 personas?
Resolución
Punto I
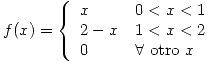
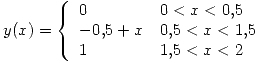
Primero voy a hallar el comportamiento de la funcion 
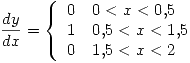
Los puntos que dividen ramas de 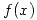 son
son 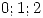
Los puntos que dividen ramas de 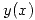 son
son 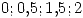
Por lo tanto tendré que analizar por separado los intervalos: 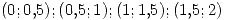
- Si
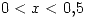
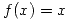 y
y 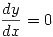
En este intervalo como la derivada tiene valor nulo, vamos a tener un punto pesado en 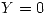
En donde 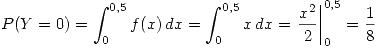
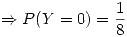 si
si 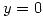
- Si
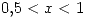
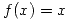 y
y 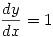
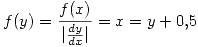
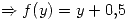 si
si 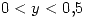
- Si
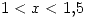
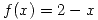 y
y 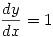
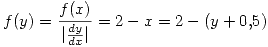
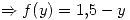 si
si 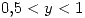
- Si
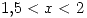
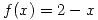 y
y 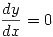
En este intervalo como la derivada tiene valor nulo, vamos a tener un punto pesado en 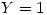
En donde 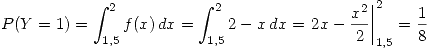
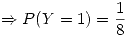 si
si 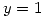
Por lo tanto la distribucion de 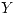 quedaría:
quedaría:
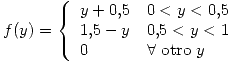
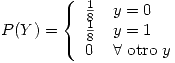
Entonces ya quedo todo preparado para calcular lo pedido en el enunciado
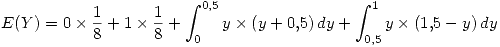
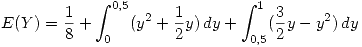
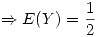
Luego:
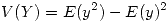
En donde: 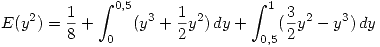
…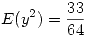
Asi lo que nos queda es:
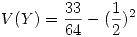
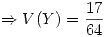
Punto II
Me están pidiendo la probabilidad de que haya cambiado al menos una vez al ejecutante. Esto lo puedo pensar como 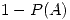 en donde
en donde 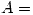 “no cambiar de ejecutante“
“no cambiar de ejecutante“
Para que no cambie nunca en los 19 partidos, el ejecutante tiene que haber marcado todos los penales a favor.
Planteo una nueva distribucion 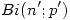 en donde
en donde  y
y  ; esto ultimo sale de la probabilidad de que haya un penal y que lo falle
; esto ultimo sale de la probabilidad de que haya un penal y que lo falle
Por lo tanto la distribucion queda: 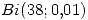
Como habia pedido antes… calculo 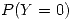 utilizando la distribucion antes dada
utilizando la distribucion antes dada
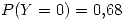 Esta sera la probabilidad de que en todo el torneo se conviertan todos los penales
Esta sera la probabilidad de que en todo el torneo se conviertan todos los penales
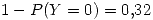
La probabiliada de que al finalizar el torneo, el mismo DT haya cambiado al menos 1 ve al ejecutatnte de penales es igual a 32%
