Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primer Recuperatorio, Primer Cuatrimestre 2006
Día: 15/06/2006
Enunciado
Punto I
Sea 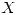 una variable aleatoria uniforme en
una variable aleatoria uniforme en  con
con  . Si
. Si 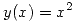 . Hallar
. Hallar  .
.
Punto II
Tres operarios 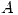 ,
, 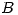 y
y 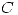 realizan c/u una tarea para completar un trabajo. Los operarios
realizan c/u una tarea para completar un trabajo. Los operarios 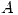 y
y 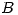 comienzan simultaneamente sus tareas y cuando terminan comienza el operario
comienzan simultaneamente sus tareas y cuando terminan comienza el operario 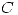 . Los tiempos en días que tarda cada operario son variables uniformes independientes
. Los tiempos en días que tarda cada operario son variables uniformes independientes 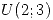 ;
;  ;
; 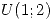 para
para 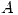 ,
, 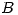 y
y 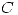 respectivamente. Encontrar la fdp del tiempo total que se insume en completar el trabajo
respectivamente. Encontrar la fdp del tiempo total que se insume en completar el trabajo
Punto III
Una carpitería recibe tablas de tres aserraderos 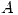 ,
, 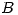 y
y 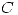 . Las longitudes en metros de las tablas que entrega c/u tiene distribución normal con los siguientes paramentros respectivamente:
. Las longitudes en metros de las tablas que entrega c/u tiene distribución normal con los siguientes paramentros respectivamente: 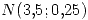 ,
,  y
y  . Encontrar la probabilidad de que la longitud de
. Encontrar la probabilidad de que la longitud de  tablas del proveedor
tablas del proveedor 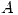 supere la longitud de
supere la longitud de 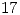 tablas del proveedor
tablas del proveedor 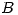 más
más 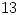 del proveedor
del proveedor 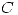 .
.
Punto IV
Se enfrentan en un partido de fútbol dos equipos con respectivas tasas de goles a favor por partido igual a uno. Que es mas probable, que el partido termine empatado o no empatado?
Resolución
Punto I
Es un cambio de variable un poco trivial, lo único que hay que tener en cuenta es que el analizando el nuevo dominio  nos damos cuenta que obtenemos dos idénticos de probabilidad
nos damos cuenta que obtenemos dos idénticos de probabilidad  y
y  ya que en esos intervalos los valores de la derivada
ya que en esos intervalos los valores de la derivada  cambia de valor ya que
cambia de valor ya que  en
en  es menor que cero y
es menor que cero y  en
en  es mayor que cero.
es mayor que cero.
Analizado por completo:
 para
para 
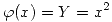
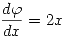
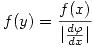 evaluado en
evaluado en 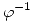
Para  ; y
; y  va a parar a
va a parar a 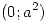 .
.
Para 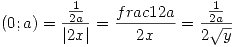 ; y
; y  va a parar a
va a parar a 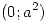 .
.
Entonces:
 , para
, para 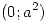
Simplificando:

Listo el pollo.
Punto II
Este es el mas largo y quiza mas complicado de desarrollar y no equivocarse con las cuentas eh!!
Primero vemos que nos dice que el chabón  no empieza hasta que no terminan
no empieza hasta que no terminan  y
y  . Entonces vemos que el hecho de que quien termine mas tarde entre
. Entonces vemos que el hecho de que quien termine mas tarde entre  y
y  nos va a dar el mayor primer tiempo, y ahí caemos que hay que sacar el máximo de los dos tiempos. Luego tenemos que a eso sumarle lo que tardara
nos va a dar el mayor primer tiempo, y ahí caemos que hay que sacar el máximo de los dos tiempos. Luego tenemos que a eso sumarle lo que tardara  y esto es un simple cambio bidimensional
y esto es un simple cambio bidimensional  .
.
Habiendo simplificado vamos a la papota:
Para conocer el maximo necesito conocer las  de
de  y
y  :
:
Como son variables independientes pero tienen distinta  , el maximo es la
, el maximo es la  (N=2 en este caso porque son dos variables), partidas en todos los minidominios que tenga (lo vemos mas adelante). Si tuviesen la misma
(N=2 en este caso porque son dos variables), partidas en todos los minidominios que tenga (lo vemos mas adelante). Si tuviesen la misma  entonces hago sumatoria y elevo a la N.
entonces hago sumatoria y elevo a la N.
Examino los dominios y veo que:

La primer multiplicación es para el primer minidomio, donde ambas  aportan probabilidad. La segunda solo aporta el muchacho
aportan probabilidad. La segunda solo aporta el muchacho  .
.

Ahora hay que sumar esto a la uniforme de  y listo. Como sabemos que son independientes las multiplicamos y obtenemos
y listo. Como sabemos que son independientes las multiplicamos y obtenemos  para
para 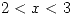 y
y 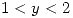 .
.
Para obtener  hago el cambio de variable:
hago el cambio de variable:

Obtengo el jacobiano de la transformación 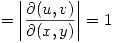 .
.
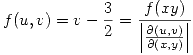
Ahora, necesito en realidad  que es
que es  . Integro
. Integro 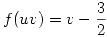 en
en 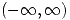 y listo, viendo el dominio, que hubo que hacerle la transformación y quedo asi, encerrado entre:
y listo, viendo el dominio, que hubo que hacerle la transformación y quedo asi, encerrado entre:

Queda algo asi:
Luego de integrar  queda partida para
queda partida para  y
y 
Las integraciones:
 termina yendo a
termina yendo a  .
.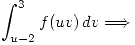 termina yendo a
termina yendo a  .
.
Punto III
Este problema es más vuelta que otra cosa, hay que usar el tema de que combinación lineal de Normales es normal y suma de normales es normal.
A saber:
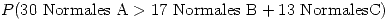 =
= 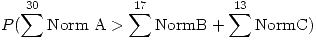


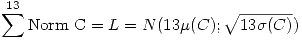
 queda
queda 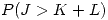
Defino  ;
;  queda
queda 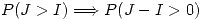
Defino 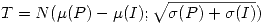 ;
;  queda
queda 
Haciendo todas las cuentas queda  y el resultado del problema es 1, que sale de hacer el cambio
y el resultado del problema es 1, que sale de hacer el cambio  y evaluar
y evaluar 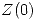 y esto lo sacamos de la tabla de Normal.
y esto lo sacamos de la tabla de Normal.
Sí, la probabilidad da 1. (Aunque ud no lo crea)