Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primera Oportunidad - Primer Cuatrimestre 2006
Día: 18/05/2006
Tema: 1
Enunciado
- La cantidad de crías que tiene una determinada especie de ave tiene dist
 ;
;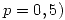 . Encontrar 1a función de probabilidad de la cantidad de nidos que habrá que inspeccionar hasta encontrar l0 nidos con al menos 2 crías.
. Encontrar 1a función de probabilidad de la cantidad de nidos que habrá que inspeccionar hasta encontrar l0 nidos con al menos 2 crías. - Sea
 una variable discreta Uniforme para
una variable discreta Uniforme para  . Sea
. Sea 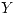 una variable discreta Uniforme para
una variable discreta Uniforme para 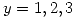 . Sean
. Sean  e
e 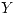 independientes. Encontrar
independientes. Encontrar  y
y  si
si  .
. - Sea
 Encontrar:
Encontrar:  y su media.
y su media. - Sea
 la cantidad de operaciones que se realizan por día en un quirófano con
la cantidad de operaciones que se realizan por día en un quirófano con 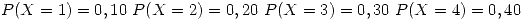 . La duración de cada operación es una exponencial de media una hora. Encontrar la función de probabilidad del tiempo diario de ocupación del quirófano.
. La duración de cada operación es una exponencial de media una hora. Encontrar la función de probabilidad del tiempo diario de ocupación del quirófano.
Resolución
Punto I
Lo que plantea el problema es la aplicación de un distribución Poisson donde la probabilidad de dicha distribución se obtiene mediante un distribución Binomial.
Se plantea  como la distribución binomial,
como la distribución binomial, 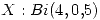 que permitirá conocer la probabilidad de encontrar al menos dos crías en un nido:
que permitirá conocer la probabilidad de encontrar al menos dos crías en un nido:
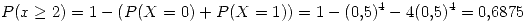
Entonces ahora 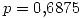 es la probabilidad de que exista un éxito de la distribución Pascal (
es la probabilidad de que exista un éxito de la distribución Pascal (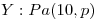 ).
).
Es decir, dada la probabilidad de encontrar al menos 2 crías en un nido, uso una Pascal para determinar cuantos nidos deberé revisar hasta obtener 10 que tengan al menos dos crías.
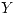 es la función de probabilidad buscada. Esta se puede escribir de la siguiente forma:
es la función de probabilidad buscada. Esta se puede escribir de la siguiente forma:

Punto II
Punto III
Se obtiene 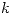 sabiendo que
sabiendo que 

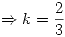
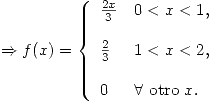
Se sabe que dadas  e
e 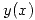 , podemos obtener
, podemos obtener  mediante:
mediante:
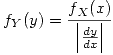
Entonces para 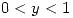
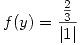
Para 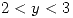

Entonces:
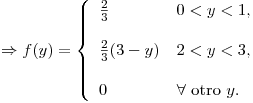

Punto IV
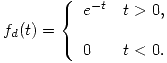
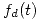 es la función de densidad de probabilidad de la duración de cada operación.
es la función de densidad de probabilidad de la duración de cada operación.
Se define  como el tiempo diario de duración.
como el tiempo diario de duración.

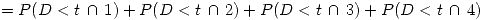
Donde  es la función de probabilidad acumulada,
es la función de probabilidad acumulada, 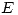 es el espacio muestral y
es el espacio muestral y 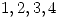 representan a los días 1,2,3 y 4 respectivamente.
representan a los días 1,2,3 y 4 respectivamente.
Luego:
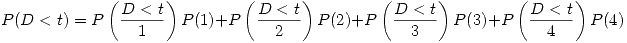
Sabiendo que al derivar la  obtenemos la función de distribución pretendida (
obtenemos la función de distribución pretendida ( ) se procede de la siguiente manera:
) se procede de la siguiente manera:
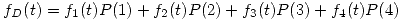
Donde 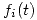 es un Gamma de variables
es un Gamma de variables  y
y 



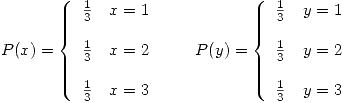
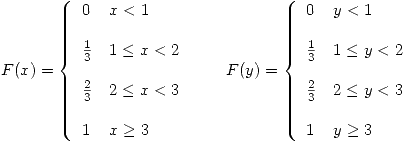
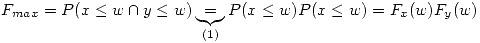
 Esta igualdad se da porque son sucesos independientes.
Esta igualdad se da porque son sucesos independientes.