Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primer Oportunidad, Primer Cuatrirmestre 2006
Día: 18/05/2006
Enunciado
Punto I
Sea 
Sea 
Encontrar  y su media.
y su media.
Punto II
Sea 
Sea 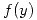 uniforme en
uniforme en 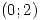 . Encontrar
. Encontrar  si
si  con
con  e
e 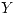 independientes.
independientes.
Punto III
Sea  la cantidad de vueltas que realiza por día un helicóptero con
la cantidad de vueltas que realiza por día un helicóptero con 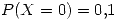 ,
,  ,
, 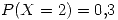 ,
,  . La duración de cada vuelo es exponencial de media 30 minutos. Encontrar la probabilidad de que el tiempo total de vuelo en un día supere las 2 horas.
. La duración de cada vuelo es exponencial de media 30 minutos. Encontrar la probabilidad de que el tiempo total de vuelo en un día supere las 2 horas.
Punto IV
La cantidad de frutos que tiene una planta tiene distribución 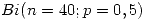 . Encontrar la función de probabilidad de la cantidad de plantas que habrá que inspeccionar hasta encontrar 5 con al menos 20 frutos.
. Encontrar la función de probabilidad de la cantidad de plantas que habrá que inspeccionar hasta encontrar 5 con al menos 20 frutos.
Resolución
Punto I
Punto II
Sea 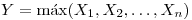 sinedo las
sinedo las 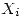 variables independientes, cada una con su propia distribución. Se define
variables independientes, cada una con su propia distribución. Se define

Donde  es la distribución de probabilidad acumulada a izquierda de la variable
es la distribución de probabilidad acumulada a izquierda de la variable 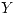 .
.
En el caso de este problema se tiene  . Entonces
. Entonces
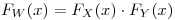



Punto III

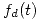 es la función de densidad de probabilidad de la duración de cada vuelo.
es la función de densidad de probabilidad de la duración de cada vuelo.
Se define  como el tiempo diario de duración.
como el tiempo diario de duración.

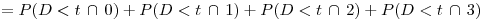
Donde  es la función de probabilidad acumulada,
es la función de probabilidad acumulada, 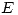 es el espacio muestral y
es el espacio muestral y  representan a las vueltas 0,1,2 y 3 respectivamente.
representan a las vueltas 0,1,2 y 3 respectivamente.
Luego:

Sabiendo que al derivar la  obtenemos la función de distribución pretendida (
obtenemos la función de distribución pretendida ( ) se procede de la siguiente manera:
) se procede de la siguiente manera:
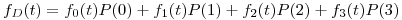
Donde 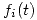 es un Gamma de variables
es un Gamma de variables 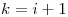 y
y 


Punto IV
En primer lugar hay que determinar el tipo de variable que vamos a usar: en este caso, una Pascal.
PAS = Cantidad de plantas a inspeccionar hasta encontrar 5 con al menos 20 frutos.

p es la probabilidad de encontrar al menos 20 frutos en un árbol ⇒ calculo p.
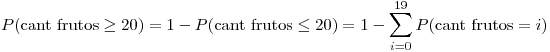
Donde 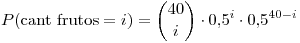
Ejemplo: 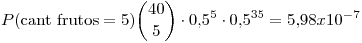

 con
con  .
.
