Examen (Parcial|Final) - 61.09. Probabilidad y estdística B

Cátedra: Gil
Fecha: 1° oportunidad - (1° Cuatrimestre 2005
Día: 01/06/2005

El diámetro (en cm) de ciertos ejes es una variable aleatoria cuya función de densidad de probabilidad es 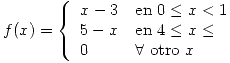. Una maquina esta diseñada para descartar ejes cuyos diámetros sean inferiores a 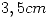o superiores a 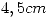. Pero a veces falla, y en un 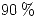de las veces descarta ejes cuyos diámetros son inferiores a y en un de las veces descarta aquellos cuyos diámetros superan los 4,5 cm. Todos los ejes cuyos diámetros están comprendidos entre 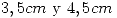no son descartados por dicha maquina. Halle la función de densidad de probabilidad de los diámetros de los ejes no descartados.

En una fabrica de el 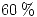de la producción son ejes y el resto son bujes. El peso de la producción es una variable aleatoria y el peso de cada eje es una variable normal de media 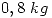y desvío 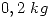a) De 4 artículos seleccionados al azar de la fabrica ¿Cúal es la probabilidad de que al menos dos no superen los 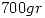? b) En una caja que vacía pesa 1 Kg se colocan 6 bujes y dos ejes. ¿Que porcentaje de cajas completas no superan los ? c) Suponga que el peso de los bujes es una variable normal de media 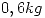. Y desvío . En una caja se colocan 2 artículos de la fabrica ¿cual es la probabilidad de que el peso de la misma sea inferior a 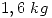? Considere despreciable el peso de la caja.

El tiempo neto (sin contar detenciones), que tarda un señor en realizar un determinado viaje es una variable aleatoria horas. Se detiene una vez a lo largo de todo el viaje, tardando un tiempo aleatorio según una distrubución minutos. Antes de comenzar el viaje, realiza los preparativos previos del mismo que le insumen un tiempo de 30 minutos. Halle la función de densidad de probabilidad y la media del tiempo que tarda el señor en realizar el viaje, incluyendo los tiempos de detención y de los preparativos previos.

La funcion de densidad de probabilidad conjunta correspondientes a la base y a la altura de una plancha triangular cortada por una maquina es: .

1. ¿Cúal es el área media de las planchas cortadas por la máquina?
2. ¿Cúal es la probabilidad de que la base sea mayor que 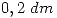, si la altura mide ?
3. La base y la altura de cada plancha, ¿son variables aleatorias independientes? Justifique.

En un proceso Poisson el número de dispositivos electrónicos que fallan en promedio cada 1000 horas es 10.

1. Determine la probabilidad de que en 200 horas fallen más de 2 dispositivos si se sabe que fallarón menos de 5 en ese lapso.
2. ¿Cúal es la probabilidad de que el tiempo hasta que fallen 3 dispositivos sea mayor que 400 horas?. Deje expresado el cálculo.
3. Si el costo de fabricar un dispositivo es de 30 $, y se incurre en un costo adicional de 10 $, y al ponerlo a prueba, falla antes de las 100 hora, ¿cúal es el costo medio de fabricación de cada dispositivo?