Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primera Oportunidad - Primer Cuatrimestre 2005
Día: 27/05/2005
Tema: 2
Enunciado
Punto I
En un proceso de fabricación que trabaja con 10% de defectuosos se producen diariamente 5, 10 o 15 piezas con probabilidades del 20%, 30% y 50% respectivamente. Al final del día se hace un control y se separan las defectuosas, pero hay una probabilidad constante del 1% de considerar buena una unidad defectuosa. ¿Cuál es la probabilidad de que en un día cualquiera se separen al menos 2 defectuosas?
Punto II
Sea H la cantidad de personas que ingresan a un ascensor, donde 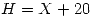 , con X Poisson de media 10. El peso en kilos W de cada persona tiene función de probabilidad
, con X Poisson de media 10. El peso en kilos W de cada persona tiene función de probabilidad 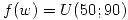 . Encontrar la exrpesion general de la función de probabilidad del peso total de las personas que ingresan al ascensor.
. Encontrar la exrpesion general de la función de probabilidad del peso total de las personas que ingresan al ascensor.
Punto III
Sea 
Si 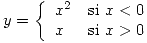
- Encontrar f(y) y E(y).
- Graficar
Punto IV
Sea 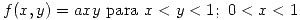
Hallar f(v) donde 
Resolución
