Tabla de Contenidos
Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primera Oportunidad - Primer Cuatrimestre 2004
Día: 19/05/2004
Tema: 3
Esta página está incompleta; podés ayudar completando el material.
Enunciado
- Sea
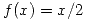 en (0;2). Si se obtienen 3 valores de x en forma independiente:
en (0;2). Si se obtienen 3 valores de x en forma independiente:- Encontrar un número m tal que la probabilidad de que al menos uno de los 3 valores de x supere a m sea 0,80.
- Encontrar la media del valor máximo de los 3 valores.
- En un carrete de piolín de 100 metros de largo hay un trozo de un metro defectuoso. Indicar la probabilidad de que los primeros 5 metros del carrete estén sanos.
- Sea
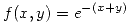 para
para  ,
,  :
:- Encontrar la probabilidad de que
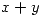 esté comprendido entre dos números a y b. Asignar a las variables x e y un significado concreto e interpretar el resultado.
esté comprendido entre dos números a y b. Asignar a las variables x e y un significado concreto e interpretar el resultado. - ¿Son x e y independientes? Justifique.
- Una urna contiene 3 tarjetas numeradas del 1 al 3. Se extraen las 3 tarjetas sin reposición:
- Calcular la media y el desvío de la variable X: “cantidad de veces que coincide el número de la tarjeta con el número de extracción”
- Encontrar la media del número de coincidencias cuando en la urna hay “n” tarjetas (ayuda: piense en x como suma de variables Bernoulli).
- Al ir a su trabajo un automovilista recorre en su primer hora de viaje una distancia X uniforme (20;30) en km. Para una distancia X dada, el rendimiento y del automóvil (en lt/km) es
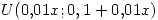 :
:- Calcular la probabilidad de que el vehículo se quede sin combustible al cabo de la hora de viaje si inicialmente el tanque contiene 10 litros y no hay posibilidad de recargarlo.
- Encontrar la f(y). Graficar.
Resolución
Discusión
Si ves algo que te parece incorrecto en la resolución y no te animás a cambiarlo, dejá tu comentario acá.
Excepto donde se indique lo contrario, el contenido de esta wiki se autoriza bajo la siguiente licencia: CC Attribution-Noncommercial-Share Alike 3.0 Unported
