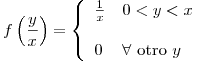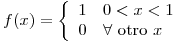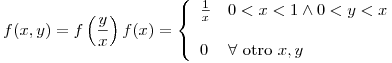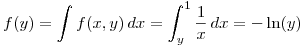Examen Parcial - 61.09. Probabilidad y Estadística B
Cátedra: Baliña
Fecha: Primer Oportunidad - Segundo Cuatrimestre 2003
Día: 31/10/2003
Enunciado
Punto I
El control de recepción de una pieza, que se recibe en cajas de 10 unidades, consiste en elegir 2 piezas de cada caja y rechazar la misma si alguna es defectuosa. El proveedor colocó en cada caja un número de unidades defectuosas que depende del resultado de arrojar un dado como sigue:
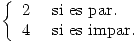
- Hallar la Función de Distribución del número de piezas defectuosas que hay en una caja.
- Calcular el porcentaje de cajas rechazadas.
Punto II
Sean
![<tex>\left\{ \begin{array}{ll} X & \mbox{ un numero al azar, } X \in [0,1] \\ Y & \mbox{ un numero al azar, } Y \in [0,X]\end{array} \right.</tex> <tex>\left\{ \begin{array}{ll} X & \mbox{ un numero al azar, } X \in [0,1] \\ Y & \mbox{ un numero al azar, } Y \in [0,X]\end{array} \right.</tex>](lib/plugins/latex/images/d7a119dfc631e366875d8c1eccbf3e99aa5a3973_0.png)
Calcular la Función de Densidad Incondicional de Y, y su Valor Esperado
Punto III
Un proceso consiste en realizar 4 operaciones. La 1 y la 2 comienzan simultáneamente. Cuando ambas terminan, y tras un día de espera, comienzan la 3 y la 4. Expresar la probabilidad de que el tiempo total de ejecución no supere los 10 días.
Resolución
Punto I
- Para hallar la función de distribución se calcula cuál es la probabilidad de que halla 2 o 4 piezas defectuosas en cada caja. La probabilidad de que salga cualquier número del dado es
 . Entonces, la probabilidad de que obtener un número impar equivale a la probabilidad de que salga el 1 o el 3 o el 5
. Entonces, la probabilidad de que obtener un número impar equivale a la probabilidad de que salga el 1 o el 3 o el 5 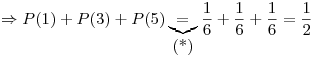 .
.
(*) Sucesos Disjuntos.
Para el caso de los pares se procede de la misma manera. Por lo tanto:
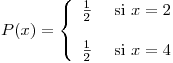
- Un caja se rechaza cuando la primer o segunda pieza que se saca, de dicha caja, es defectuosa. Vale alcarar que en el caso de ser rechazada en segunda instancia, la primer pieza obtenida es NO defectuosa; de otra forma la caja ya habría sido descartada. Para la resolución del inciso se proponen los sucesos:
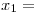 primer pieza es defectuosa y
primer pieza es defectuosa y 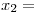 segunda pieza es defectuosa. Entonces, la probabilidad a calcular se puede expresar de la siguiente manera:
segunda pieza es defectuosa. Entonces, la probabilidad a calcular se puede expresar de la siguiente manera: 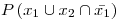
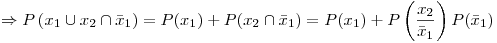
Para continuar con el ejercicio se definen dos sucesos más: 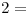 2 defectuosas en la caja, y
2 defectuosas en la caja, y 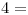 4 defectuosas en la caja.
4 defectuosas en la caja.
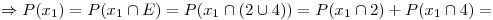
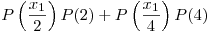
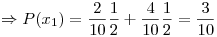
Para calcular 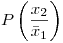 se procede de la misma manera. Sin embargo para este caso se debe tener en cuenta que ya se retiró una pieza sana de la caja.
se procede de la misma manera. Sin embargo para este caso se debe tener en cuenta que ya se retiró una pieza sana de la caja.
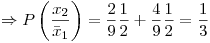
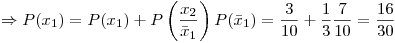
Porcentaje de cajas rechazadas: 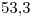
Punto II