61.09. Probabilidad y Estadística B - Guía de Ejercicios Marzo 2006 - 1. Teoría de Probabilidad
- Ejercicio 17
  - Enunciado
  - Resolución

61.09. Probabilidad y Estadística B - Guía de Ejercicios Marzo 2006 - 1. Teoría de Probabilidad

Una nave no tripulada se dirige al planeta Venus y tiene una probabilidad 0,7 de descender satisfactoriamente. A su vez, el sistema monitor da la información correcta con probabilidad 0,9 (sea o no satisfactorio el descenso). En la prueba, el monitor informó que el descenso era correcto. ¿Cuál es la probabilidad de que realmente lo haya sido?

Resolución

$<tex>c</tex>$ : descendió correctamente.
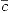$<tex>\overline{c}</tex>$ : descendió incorrectamente.
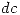$<tex>dc</tex>$ : Se informó correctamente el descenso.
$<tex>\overline{dc}</tex>$ : Se informó incorrectamente el descenso.
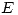$<tex>E</tex>$ : Espacio muestral.

La incognita del problema es: 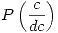$<tex>P\left( \frac{c}{dc}\right)</tex>$

Se sabe que:

$<tex>P \left( \frac{c}{dc} \right) = \frac{ P(c \cap dc) }{ P(dc) } = \frac{ P(c \cap dc) }{ P(dc \cap E) } = \frac{ P(c \cap dc)}{ P( dc \cap (c \cup \overline{c})) } = \frac{ P(c \cap dc) }{ P(dc \cap c) + P(dc \cap \overline{c}) }</tex>$

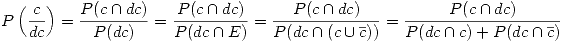
Lo que queda ahora planteado es el teorema de Bayes:

$<tex>P \left( \frac{c}{dc} \right) = \frac{ P\left( \frac{dc}{c}\right)P(c)}{ P\left( \frac{dc}{c}\right)+ P\left( \frac{dc}{\bar{c}}\right)P(\bar{c})} = \frac{0,9 \times 0,7}{0,9 \times 0,7 + 0,1 \times 0,3}= 0,9 \hat{45}</tex>$

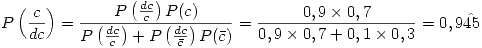
Con esto, la probabilidad de que realmente haya sido correcto el descenso es de $<tex>94.\hat{54} \%</tex>$

61.09. Probabilidad y Estadística B - Guía de Ejercicios Marzo 2006 - 1. Teoría de Probabilidad

Ejercicio 17

Enunciado

Resolución