Enunciado
- Punto I
- Punto II
- Punto III
- Punto IV
- Punto V

No estoy seguro si estos enunciados son 100% exactos, pero según recuerdo eran así. La ídea básica está.

Enunciado

Punto I

Calcular $<tex>E[cos(\pi X)]</tex>$ para una variable aleatoria X cuya función de distribución tiene el siguiente gráfico.

La distribución de (X,Y) es uniforme sobre la suma de los cuadrados definidos por 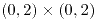$<tex>(0,2)\times(0,2)</tex>$ y $<tex>(-2,0)\times(0,-2)</tex>$ . Hallar la densidad conjunta de $<tex>(U,V) = (|X|, |Y|)</tex>$

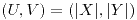
Punto III

Llamadas arriban al 911 según una Poisson de intensidad 60 por hora. A las 0:00 un oficial se fue a fumar durante un tiempo exponencial de media 5 minutos, independiente de los arribos de llamadas. Sabiendo que durante ese tiempo arribo alguna llamada al 911 calcular la probabilidad de que la primera llamada haya arribado antes de las 0:05.

Punto IV

Una fábrica embotella agua de 2 fuentes A y B. Cada botella contiene agua de una sola fuente. La cantidad de renacuajos por litro en el agua es una variable Poisson con media 10, y de la fuente B con media 6. Se inspeccionaron 3 botellas con agua de la misma fuente desconocida y se encontraron 12, 9 y 11 renacuajos. Determinar por Máxima Verosimilitud la fuente de la que proviene el agua de dichas botellas. (Aclaración del profesor: Las botellas son de 1 litro)

Punto V

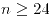En una urna hay $<tex>n</tex>$ bolas negras. Candy afirma que $<tex>n\ge24</tex>$ . Se agregan 10 bolas rojas. Luego se realizan 100 extracciones de una bola con reposición y se observan 28 rojas. ¿Se puede rechazar la afirmación de Candy con nivel de significación de $<tex>\alpha=0.1</tex>$ ?