Examen Final - 61.09. Probabilidad y Estadística B - 23/07/2008
Cátedra: Todas
Fecha: Tercera Fecha Final - Primer Cuatrimestre 2008
Día: 23/07/208
Tema: 2
Enunciado
- Se tienen dos monedas. Una moneda está cargada con probabilidad
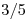 de salir “cara” y la otra con probabilidad
de salir “cara” y la otra con probabilidad 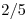 . Puede optar por una de las siguientes estrategias: (E1) Elegir una moneda al azar y lanzarla dos veces. (E2) Lanzar ambas monedas. El juego se gana si salen 2 “caras”; en caso contrario se pierde. ¿Cuál de las dos estrategias es más conveniente?.
. Puede optar por una de las siguientes estrategias: (E1) Elegir una moneda al azar y lanzarla dos veces. (E2) Lanzar ambas monedas. El juego se gana si salen 2 “caras”; en caso contrario se pierde. ¿Cuál de las dos estrategias es más conveniente?. - Sea
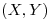 con distribución uniforme en el cuadrado de vértices
con distribución uniforme en el cuadrado de vértices 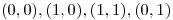 .
.
Sea
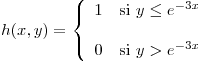
Hallar la media y la varianza de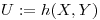
- El precio de uso de un teléfono es de 25 centavos por pulso. Los pulsos se cuentan cada dos minutos o fracción. Las llamadas tienen duración exponencial de media 3 minutos. (a) Puede verse que la cantidad de pulsos de una llamada es una variable aleatoria geométrica de parámetro p. Hallar p. (b) Hallar la media y la varianza del costo de cada llamada.
- La cantidad de litros de vino consumidos anualmente por cada cliente de una bodega tiene distribución normal con desvío 18 litros. La bodega planea innovar su línea de vinos siempre y cuando pueda asegurarse una venta media de no menos de 100 litros por cliente. Envía algunas botellas “gratis” a 16 clientes de confianza, quienes deberán contestar cuántos litros estarían dispuestos a consumir. En base a esos resultados decidirá qué hacer. Si el consumo medio fuese de 105 litros per capita, estaría dispuesta a correr un riesgo del 5% de no innovar.
Diseñar un test y describir una regla de decisión para esta situación, graficar la curva característica operativa. Si la bodega decidiese no innovar, cuál sería la máxima probabilidad de haberse equivocado. - Se tienen dos dados. Uno equilibrado y otro con probabilidad de as
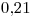 . Se elige un dado y se lo lanza 5 veces. Se observan 2 ases. Hallar el estimador de máxima verosimilitud de la probabilidad de as.
. Se elige un dado y se lo lanza 5 veces. Se observan 2 ases. Hallar el estimador de máxima verosimilitud de la probabilidad de as.
Resolución
Punto 1
La estrategia más conveniente será aquella para la cual la probabilidad de ganar sea mayor.
(E1) Es un experimento de varias etapas. Para calcular la probabilidad se puede hacer un diagrama de árbol o usar probabilidad compuesta. Sean los eventos: M1=“Se eligió la moneda cargada con p=3/5”; M2=“Se eligió la moneda cargada con p=2/5”; H1=“Cara en el primer lanzamiento”; T1=“Ceca en el primer lanzamiento”; H2=“Cara en el segundo lanzamiento”; T2=“Ceca en el segundo lanzamiento”;
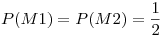
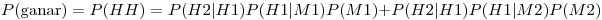
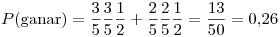
(E2) Como el lanzamiento de una moneda es independiente del lanzamiento de la otra,
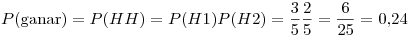
La estrategia más conveniente resulta ser (E1).
Punto 2
![<tex>E[U]=E[h(X,Y)]=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} h(x,y)f_{XY}(x,y) \,dydx</tex> <tex>E[U]=E[h(X,Y)]=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} h(x,y)f_{XY}(x,y) \,dydx</tex>](lib/plugins/latex/images/4cc607120fd2074a2abfa776109a8d266220c60a_0.png)
![<tex>V[U]=E[U^2]-(E[U])^2</tex> <tex>V[U]=E[U^2]-(E[U])^2</tex>](lib/plugins/latex/images/20b2c33549b1231067f7fbe051b7decb7aa5aaf7_0.png)
![<tex>E[U^2]=E[(h(X,Y))^2]=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (h(x,y))^2 f_{XY}(x,y) \,dydx</tex> <tex>E[U^2]=E[(h(X,Y))^2]=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (h(x,y))^2 f_{XY}(x,y) \,dydx</tex>](lib/plugins/latex/images/0097585ece0ab32b291574656ddf1c6d885668b0_0.png)
El resto son cuentas. También se puede pensar a U como una variable que sólo toma los valores 0 y 1 y calcular la esperanza a partir de eso.
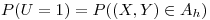 ;
; 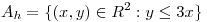
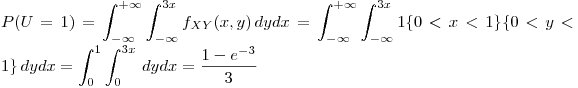
![<tex>E[U]=\sum_u uP(U=u)=0P(U=0)+1P(U=1)=P(U=1)=\frac{1-e^{-3}}{3}</tex> <tex>E[U]=\sum_u uP(U=u)=0P(U=0)+1P(U=1)=P(U=1)=\frac{1-e^{-3}}{3}</tex>](lib/plugins/latex/images/d411c6a62f38470ceb021d3562c689c337ba5fa6_0.png)
![<tex>E[U^2]=\sum_u u^2P(U=u)=1P(U=1)=\frac{1-e^{-3}}{3}</tex> <tex>E[U^2]=\sum_u u^2P(U=u)=1P(U=1)=\frac{1-e^{-3}}{3}</tex>](lib/plugins/latex/images/70067b689952be7d913651c22d96e3734658a031_0.png)
![<tex>V[U]=E[U^2]-(E[U])^2=\frac{1-e^{-3}}{3}-(\frac{1-e^{-3}}{3})^2</tex> <tex>V[U]=E[U^2]-(E[U])^2=\frac{1-e^{-3}}{3}-(\frac{1-e^{-3}}{3})^2</tex>](lib/plugins/latex/images/f9ca1c0d6e5ea5cff5d359ae4641071343f571cb_0.png)
Punto 3
Sea  la cantidad de pulsos en una llamada telefónica;
la cantidad de pulsos en una llamada telefónica; 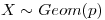 .
.
Sea  la duración en minutos de una llamada telefónica;
la duración en minutos de una llamada telefónica; 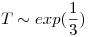 .
.
Una llamada contiene un solo pulso si su duración no supera los dos minutos. Entonces, 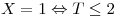
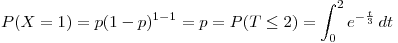
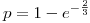
Sea  el costo de una llamada;
el costo de una llamada; 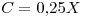
![<tex>E[C]=E[0.25X]=0.25E[X]=\frac{1}{4}p</tex> <tex>E[C]=E[0.25X]=0.25E[X]=\frac{1}{4}p</tex>](lib/plugins/latex/images/f8fa4056b8a334dcb52b6f8cce403517148133c6_0.png)
![<tex>V[C]=V[0.25X]=0.25^2V[X]=\frac{1}{16} \frac{(1-p)}{p^2}</tex> <tex>V[C]=V[0.25X]=0.25^2V[X]=\frac{1}{16} \frac{(1-p)}{p^2}</tex>](lib/plugins/latex/images/367afff31a48a5aeb1697910400b7a7c5d2a699f_0.png)
Punto 4
Sea 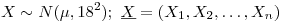 .
.
Las hipótesis a ensayar son:

El volumen de la muestra está prefijado, y es  .
.
Para poder decidir nos basamos en la información que nos arroje la muestra. Como se trata de la media de una distribución, sería coherente utilizar el promedio muestral 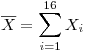 .
.
La regla de decisión sería algo así como se rechaza innovar si el promedio de litros consumidos por cliente es suficientemente menor que 100. Más formalmente,
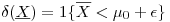
Para analizar los riesgos calculamos la curva característica operativa:
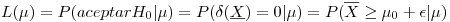
Dado que 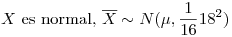 , y
, y 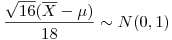
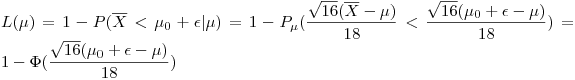
Nos dicen que para 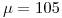 se está dispuesto a no innovar con un riesgo del 5%. Si la media es 105, vale la hipótesis nula y se debe innovar. Entonces,
se está dispuesto a no innovar con un riesgo del 5%. Si la media es 105, vale la hipótesis nula y se debe innovar. Entonces,
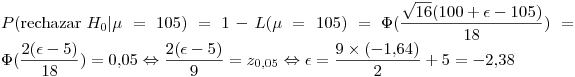
La curva característica operativa queda
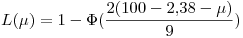
Esta función es creciente con 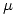 creciente, ya que la función de distribución de la normal
creciente, ya que la función de distribución de la normal 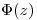 es creciente con
es creciente con  creciente y
creciente y 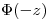 resulta decreciente con
resulta decreciente con  creciente.
creciente.
Se puede comprobar que:
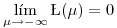 y
y 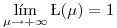
Decidir no innovar es rechazar la hipótesis nula. La probabilidad de haberse equivocado es la probabilidad de rechazar dicha hipótesis dado que la media es mayor o igual que 100. Como la curva característica es una función creciente, la máxima probabilidad será cuando 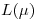 sea lo más chica posible dentro de la hipótesis nula y
sea lo más chica posible dentro de la hipótesis nula y 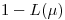 sea lo más grande posible.Esto ocurre cuando
sea lo más grande posible.Esto ocurre cuando 
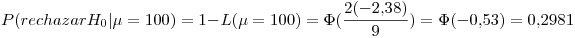
La regla de decisión queda
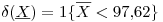
i.e., rechazar innovar si el promedio muestral es menor que 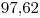 .
.
Punto 5
En palabras, lo que están pidiendo es estimar si se tiró el dado cargado o el equilibrado, habiéndose observado 2 ases.
El lanzamiento de un dado observando si el resultado es o no as, es un experimento de Bernoulli. Entonces, sea 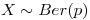 ,
, 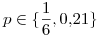 , y sea
, y sea 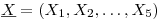 una muestra aleatoria de la variable
una muestra aleatoria de la variable  .
.
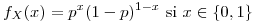
El estimador de máxima verosimilitud será el valor de p que maximice la función de verosimilitud.
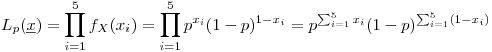
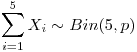 , i.e., es la cantidad de éxitos (ases) observados en 5 lanzamientos de un dado. Por lo tanto,
, i.e., es la cantidad de éxitos (ases) observados en 5 lanzamientos de un dado. Por lo tanto, 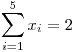

Para encontrar el máximo en este caso no hay que tomar logaritmo y derivar, sino que como p puede tomar sólo dos valores basta con evaluar la función de verosimilitud en esos valores y comparar.
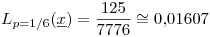
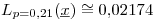
Finalmente,  .
.
