Examen Final - 61.09. Probabilidad y Estadística B - 10/07/2008
Cátedra: Única
Fecha: 1º Oportunidad - (1º Cuatrimestre 2008)
Día: 10/07/2008
Tema: 2
Enunciado
Punto 1
En una urna hay 3 bolas rojas y 2 bolas negras. En cada paso se extrae una bola al azar y si es negra se la reemplaza en la urna por una roja. Encontrar la funcion de probabilidad de la cantidad de pasos necesarios para sacar una bola roja.
Punto 2
Sea (X,Y) un punto aleatorio con distribucion uniforme en el cuarto de círculo de radio 1 centrado en (0,0) contenido en el primer cuadrante.
( a ) Hallar las densidades marginales de Y
( b ) Hallar la densidad condicional de X dado que Y = 1/2
( c ) Hallar la funcion distribución de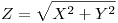 
Punto 3
A un contador Geiger arriban pulsos de acuerdo con un proceso de Poisson a tasa de 4 arribos por segundo. Cada partícula que arriba al contador tiene una probabilidad 1/2 de ser registrada. Sea X(t) el número de pulsos registrados en t segundos.
(a) P( X(t) = 0 ) = ? (b) E[ X(t) ] = ?
Punto 4
Sea X una variable aleatoria con funcion de densidad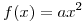 
para 0 < x < b. Encontrar la relación entre a y b. A priori, los valores de a estan distribuidos uniformemente entre 0 y 2. Si se obtuvieron los valores muestrales 0.2, 0.8 y 3 hallar la función de distribución a posteriori de a.
Punto 5
Los siguientes datos, en cientos de millones de pesos, corresponden a la facturación total del año 2007 de 10 empresas de productos alimenticios: 5.15, 5.04, 4.60, 3.42, 3.36, 3.14, 2.84, 2.65, 2.50, 2.34
( a ) Construya intervalos de confianza de nivel 0.95 para la media y la varianza, suponiendo que las ventas anuales de las empresas del sector se distribuyen con una ley normal.
( b ) ¿Rechazaría la siguiente afirmación: “En media, las ventas anuales de cada empresa del sector son de 425 millones de pesos”?, ¿Qué riesgo corre de haberse equivocado?
